Két jelentős felfedezést vagy találmányt szoktak emlegetni, ami megváltoztatta az emberiség életét, az egyik a tűz, a másik a kerék. Ebben a blogunkban az égési szimulációval foglalkozok FloEFD kezelőfelületén belül. A FloEFD a Siemens tulajdonában álló Mentor Graphics terméke, így a Siemens CAD szoftvereiben elérhető szimulációs szoftver. Nálam Solid Edge-en belül fut, de sem tudásban, sem kezelőfelületben nem különbözik az NX-es változattól.

Az égési folyamat egy komplex fizikai és kémiai folyamat, melyet a termodinamika, reakciókinematika és az áramlástan tudománya ír le. Ezeknek a tudományágaknak az egyenletrendszereit felhasználva numerikus áramlástani szimuláció segítségével az égés és az égés során lezajlódó folyamatok szimulálhatók, így nem szükséges “papíron” számolni és prototípusokat építeni. A FloEFD jó pár verzió óta gázok égését tudja vizsgálni. Amennyiben egy vagy több folyadék és gáz égését szeretnénk vizsgálni, akkor az általunk is forgalmazott Star-CCM+-mel lehetséges, ami a Siemens high-end CFD-s szimulációs szoftvere. Bármelyik szoftvert választom, az első lépés minden esetben az áramló közegek kiválasztása. A szimuláció futtatásához minden esetben szükséges tüzelőanyagot és oxidálószert kiválasztani. Erre a két közegre a CFD szoftver, jelen esetben a FloEFD meghatározza az áramlástani tulajdonságaikat, és a keveredésük közben létrejövő elegy tulajdonságait.

Az égési folyamatok a lángképzés alapján három kategóriába sorolhatók, melyek az előkevert, részlegesen előkevert és nem előkevert, azaz diffúz láng.

Előkevert és nem előkevert égés

Teljesen előkevert esetben az égéstérbe lépés előtt, már előkeverik a tüzelőanyagot és az oxidálószert, míg nem előkevert esetben a tüzelőanyag és az oxidálószer az égési térben találkoznak. Amennyiben meg van az égés és az éghető közeg és hozzá a szikra/hőmérséklet, abban az esetben a kémiai folyamatok lezajlódnak és a két közegből, az üzemanyagból (F) és az oxidálószerből (O) égési termék (P) keletkezik.

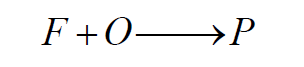
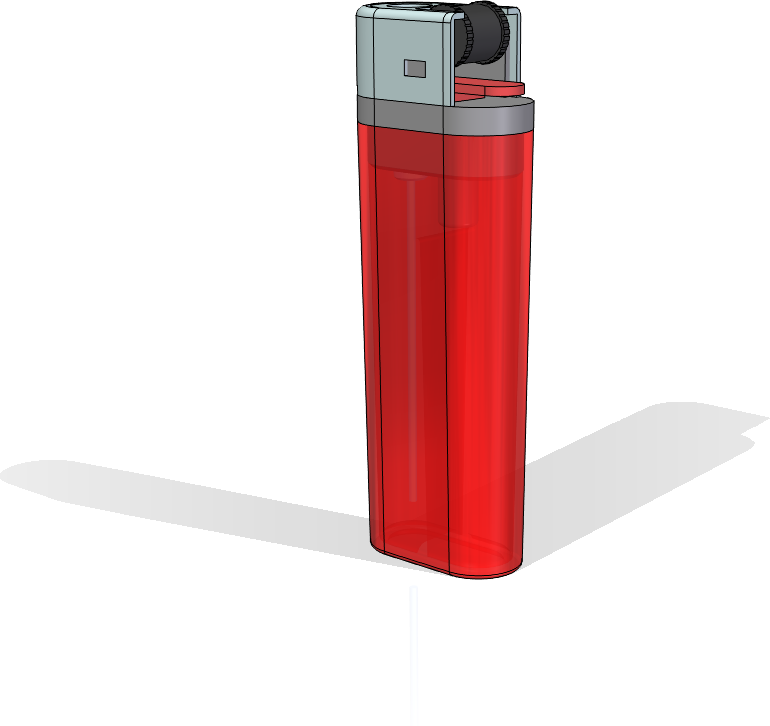
Az égési szimulációhoz egy öngyújtót választottam. A modellt a szimulációhoz a GrabCAD-en találtam modellt. Ezt követően elkezdtem keresni azt, hogy mennyi lehet a gáz sebessége amikor kilép az öngyújtóból, vagy a tömegárama, vagy a térfogatárama vagy bármilyen ilyen érték után és találtam egy piaci rést… Így nem tudtam meg, hogy mennyi a kiáramlás értéke. Ezek után arra gondoltam, hogy keresek a YouTube-on egy videót és onnan megsaccolom a sebességet. Videót találtam, de ezzel sem jutottam előrébb, így az AHS, azaz az AHogy Sikerül szabvány szerinti értéknél döntöttem.

 

Ennyi félrement keresés után, viszont a Wikipédián megtaláltam, hogy az öngyújtóban többnyire bután a tüzelőanyag. Ennek megörültem és egyből betöltöttem a szimulációhoz a letöltött modellemet és némi geometriai egyszerűsítés után a következőt modellt használtam:

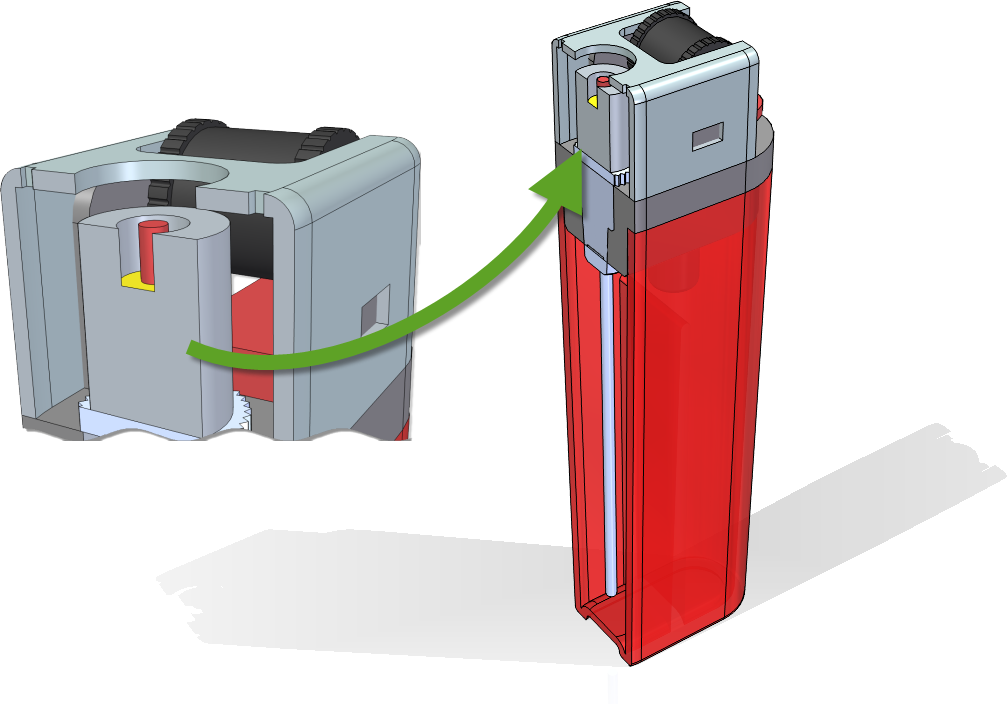
A modellből néhány letörést, lekerekítés illetve a bepattanó kötést távolítottam el, illetve az áramtér egyszerűsítése miatt modelleztem hengeres kiáramló csatornát a burkoló lemez tetejéig, és annak a közepére egy “szikrát”.

 

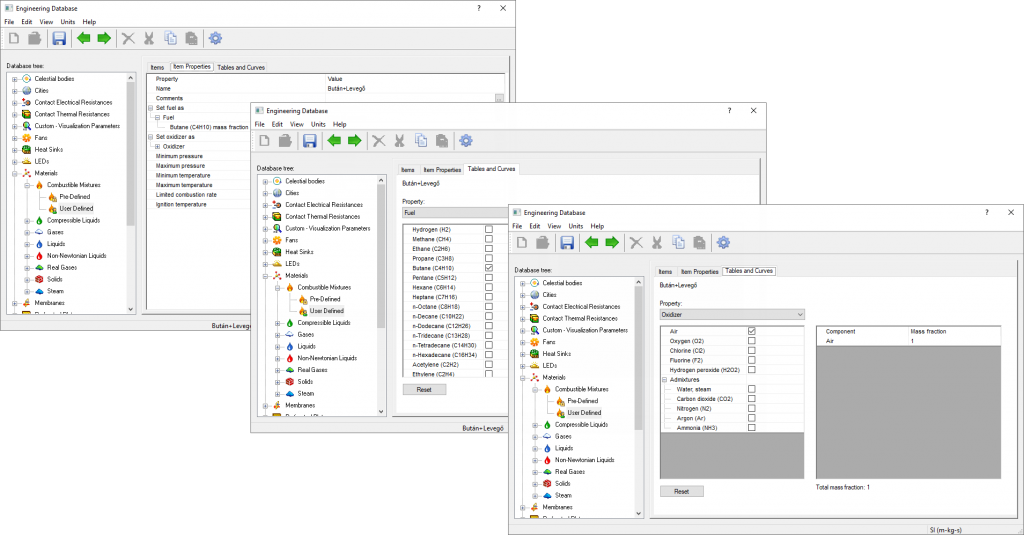
Ezek után elindítottam a FloEFD-t és a beépített adatbázison belül készítettem egy saját bután+levegő anyagot, amihez semmilyen megerőltető keresésre nem volt szükségem, az adatokat egy az egyben kimásoltam a Wikipédia Bután cikkéből. Ez az égéshő és az öngyulladási hőmérsékletek voltak, majd az anyagdefiniálás során az előre elkészített anyagmodelleket kellett összekattintanom, (amik a kezelőfelület mögött tartalmazták az anyagok kémiai és fizikai tulajdonságait).

Ezt követően a FloEFD automatikus áramtérkészítése segítségével egy külső teres szimulációt hoztam létre, ahol a hő gravitációt bekapcsoltam, a környezeti nyomás 1 atm és a környezeti hőmérséklet 20°C volt. Az áramlási teret a szimuláció elején teljes mértékben kitöltötte az oxidálószer, azaz a levegő. A számolási tartomány szélén környezeti nyomást állítottam be, a közeg onnan be és az áramlási tartományból ki szabadon áramolhat ki-be. A szimuláció során van lehetőség az NOx számítására is. Öngyújtó esetén nem éreztem ezt fontosnak, így ezt az opciót nem kapcsoltam be, viszont egy turbina, katalizátor vagy hasonlóan összetettebb szerkezetek és gázok reakciójánál bekapcsoltam voltam.

Ezt követően két peremfeltételt adtam meg. Az egyik az előző képeken látható piros hengerrel modellezett szikra volt. Ez a henger/szikra 100 W hőmérsékletet adott le az áramlási térben, ami a szimuláció 0,05 másodperce és a 0,065 másodperce között történt.

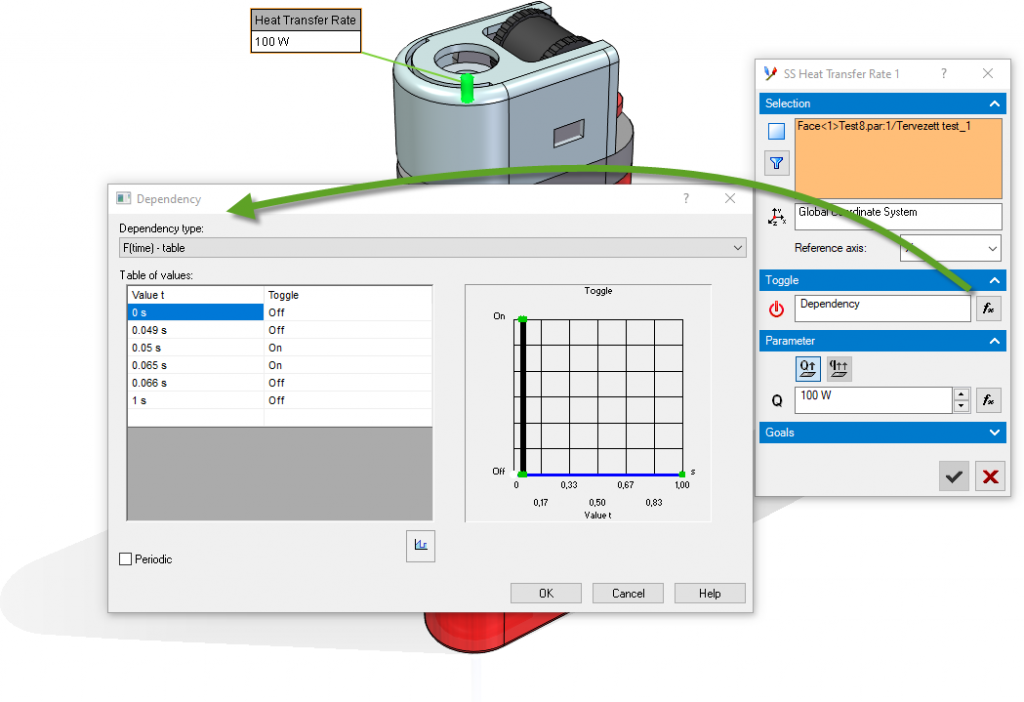
Ezt követően szintén időfüggvénnyel definiáltam az éghető gázt, amiről írtam az elején, hogy nem találtam meg. Az időfüggvényem a következő ábrán látható szerint 0 másodperctől, 0,7 másodpercig konstans tömegárammal lép ki a kiválasztott felületen (a metszeti ábrán sárgával jelölt sík felület), majd 0,7-től 0,9 másodpercig lineárisan csökken 0 gramm/másodperc tömegáramra. Ezt követően a szimuláció végéi 0 marad az értéke.

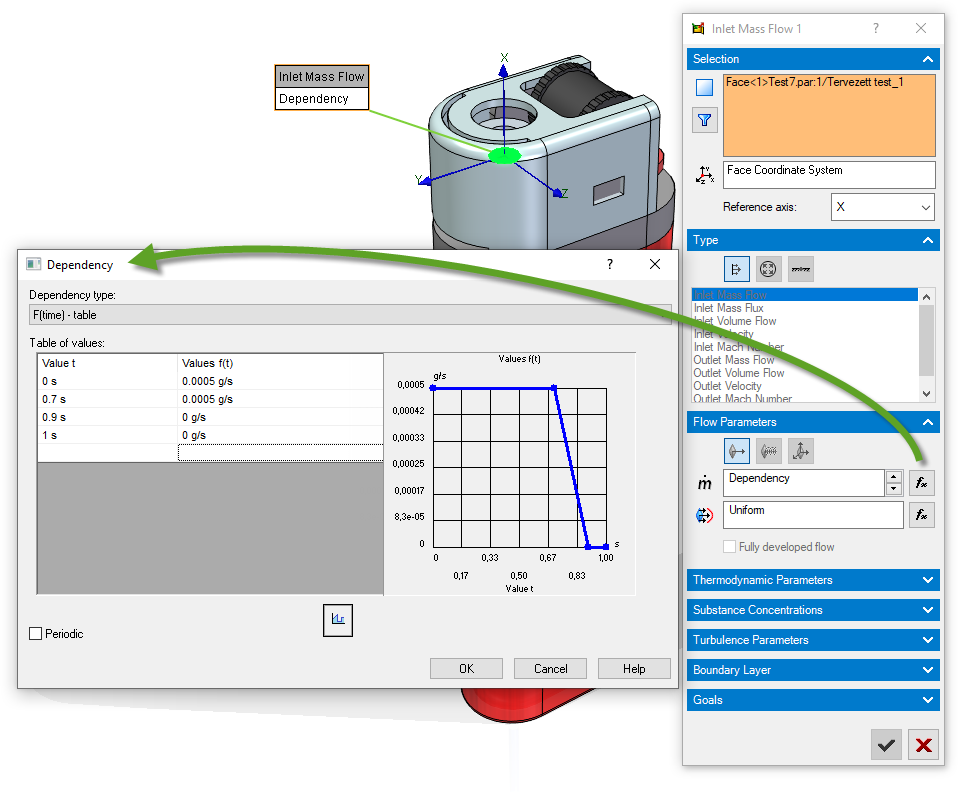
A legnagyobb áramlási sebesség meghatározásához kb. 8-szor 10-szer újrafuttattam a szimulációt, vagy futás közben módosítottam az áramlási sebességet. Első tippre 1 g/s volt a tömegáram, majd azt fokozatosan csökkentettem 0,0005 g/s tömegáramig. Erre azért volt szükség, mert a szimuláció futása közben grafikusan és parametrikusan is nyomon tudtam követni és láttam a szimulált értéket. Eleinte éreztem, hogy túl nagy hőmérsékletek jöttek ki, majd 0,001-0,001 g/s tömegáramnál már jónak tűnt. A karantén alatti otthoni munkavégzésnek köszönhetően ezeknél az értékeknél kimentem a konyhába és a konyhai gázgyújtómat gyújtogattam be és azt néztem, hogy kb. mekkora lehet az a távolság ahol már fáj a láng közelsége. Ezt követően a barátnőmmel kinéztünk egy távolságot (szemre) és ott a hőmérsékletet (kéz odatartással) megtippeltük. A “validációs” távolság így kb. 25 cm lett, és 70°C-t feltételeztünk oda.

Ezek után a tömegáramot csökkentettem 0,0003 g/s-ra és a számolási tartomány magasságának beállítottam a 25 cm-t és lefuttattam a szimulációt.

A következő videóban a sebesség, hőmérséklet, és az égéstermékek eloszlása látható az idő függvényében:

A lefuttatott szimulációt lementettem 0,5, 0,7, 0,75, 0,9 és 1 másodpercnél. A következő képeken ezeknek az állapotoknak az összehasonlítása látható.

Bután égésekor keletkező hő:

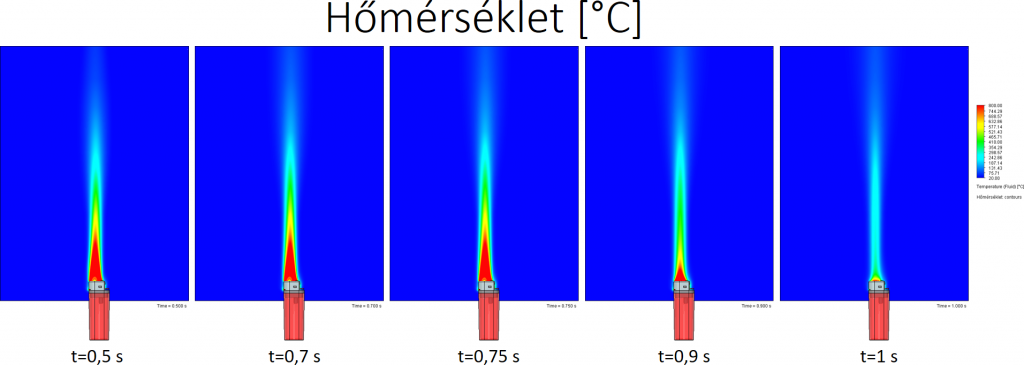
Áramlási sebesség:

 

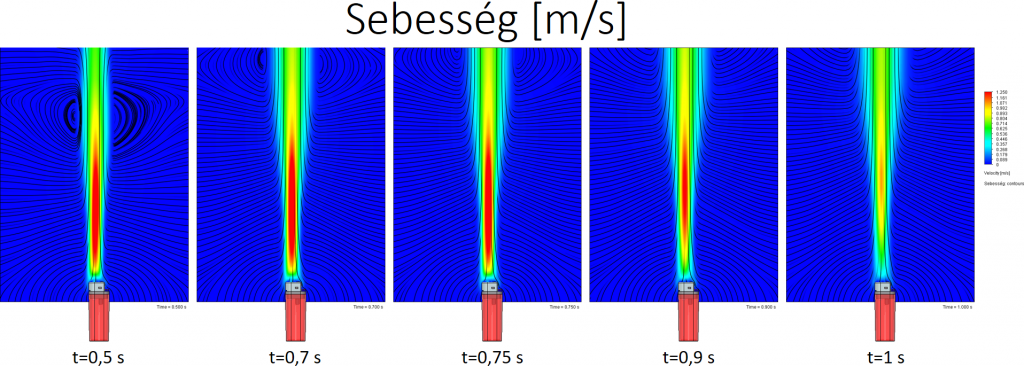
Bután égésekor keletkező CO₂ tömegaránya:

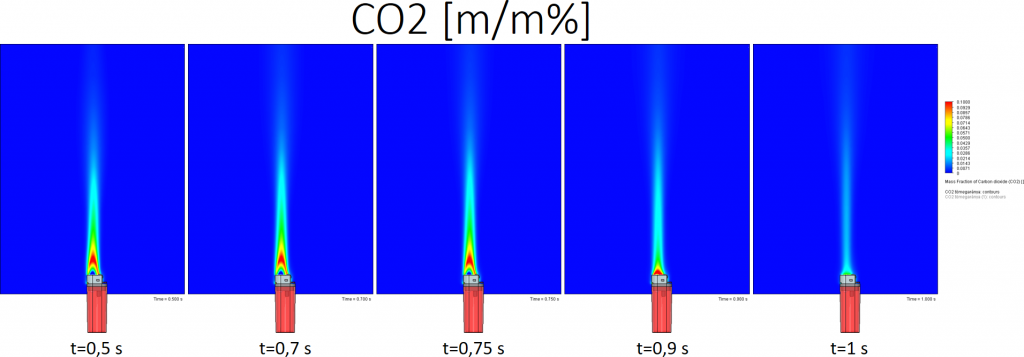
A színskála tetején a piros szín 10% vagy annál több CO₂ m/m%-ot jelent.

Bután égésekor keletkező CO tömegaránya:

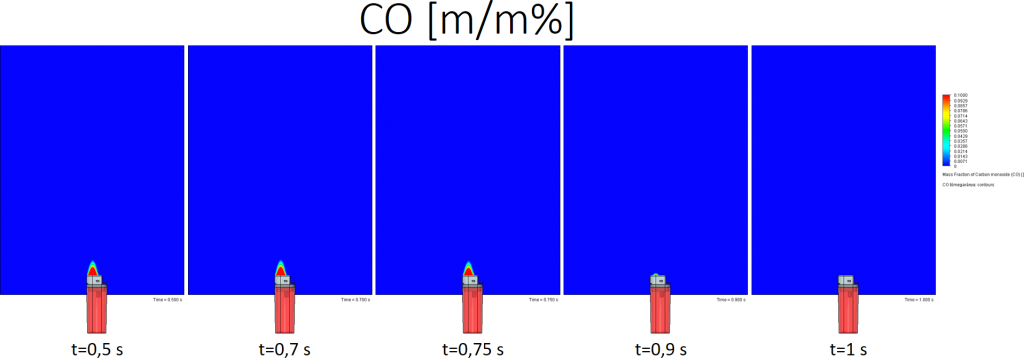
A színskála tetején a piros szín 10% vagy annál több CO m/m%-ot jelent.

Tökéletes égés esetén szénmonoxid, azaz CO nem keletkezik. Az általam beállított peremfeltételek esetén a térben, a nem kékkel jelölt részen CO keletkezett.

Bután égésekor keletkező víz tömegaránya:

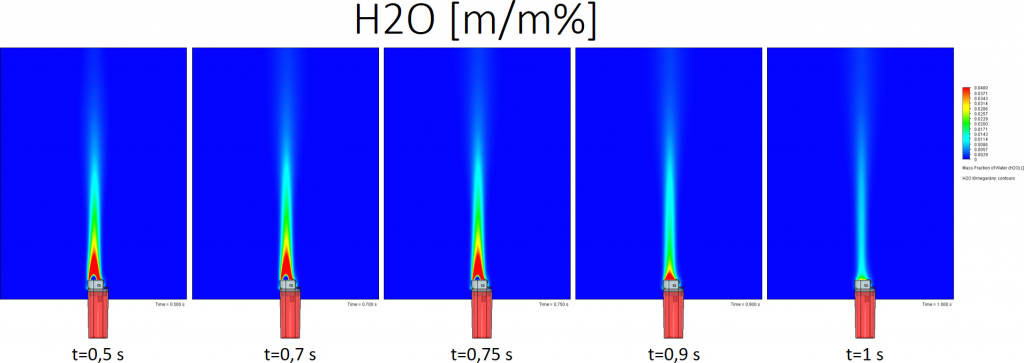
A színskála tetején a piros szín 4% vagy annál több víz tömegarányt jelent.

Az előző plot magyarázata az, hogy a bután égésekor széndioxid és víz keletkezik. Egyensúlyi helyzetben a következő egyenlet szerint:

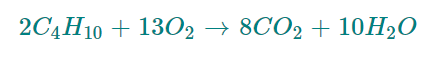
Tüzelőanyag tömegaránya:

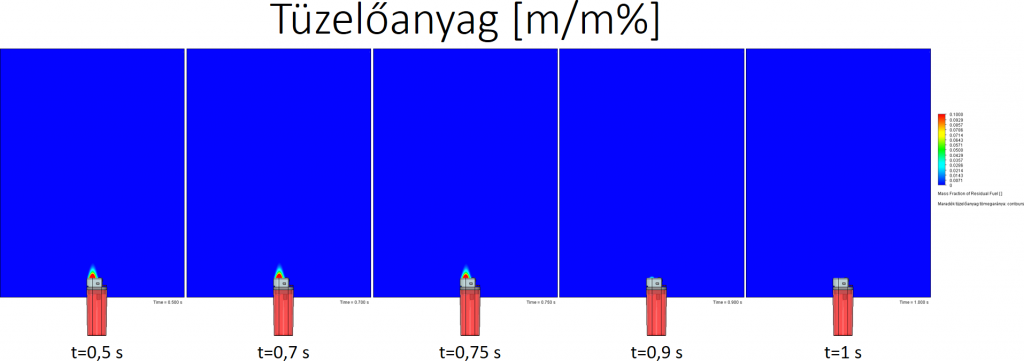
Égéstermék/elégetett tüzelőanyag tömegaránya (a középsíkban):

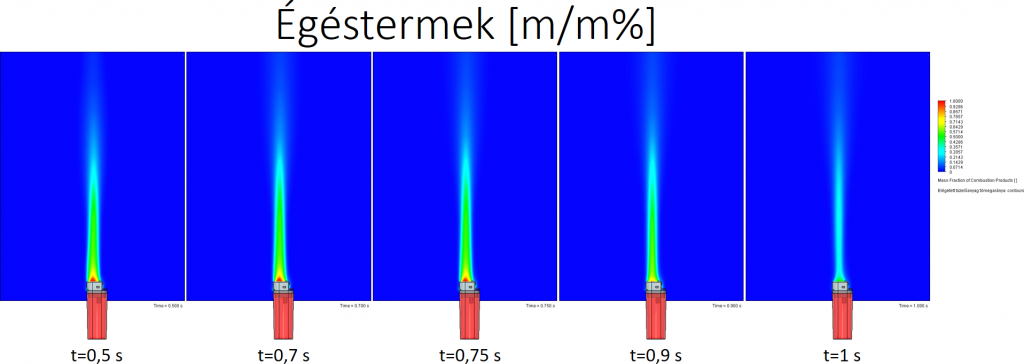
Égéstermék/elégetett tüzelőanyag tömegaránya (a térben):

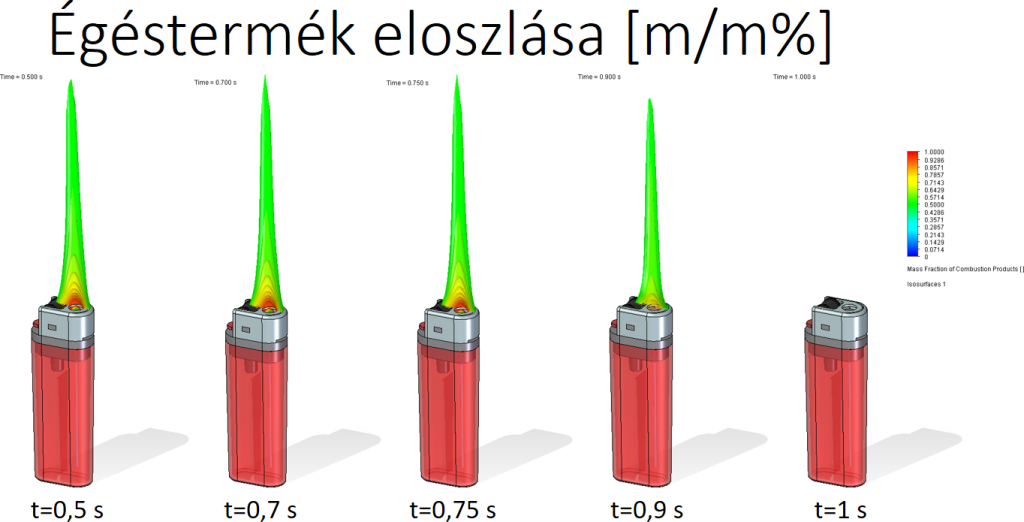
A jobb szemléltethetőség miatt 50-100%-ig vannak ábrázolva az eredmények.

 

Ebből a szimulációból sokat tanultam. Első körben azt, hogy én középiskolában tanultam utoljára kémiát (főiskola alatt ebből a tudásból éltem meg), és sokat felejtettem. Erre a H₂O plotolásánál jöttem rá, amikor szembesültem azzal, hogy a bután (C₄H₁₀) égésekor minden alkotóelem megvan a víz képződéséhez. Ezek után végiggondoltam, hogy ha nem ezt az öngyújtót és a benne lévő gázt választom, hanem egy turbinát, egy lángszórót, egy konyhai gáztűzhely gázégőjét akkor talán észre sem veszem, hogy keletkezik vízgőz. Szóval örülök, hogy a FloEFD tartalmaz égési szimulációt és ezzel játszva tanultam ma is valamit.

 

Források

• [1] Premixed Versus Non-Premixed Flames, https://dustsafetyscience.com/premixed-vs-non-premixed-flames/
• [2] GrabCAD modell, https://grabcad.com/library/plastic-lighter-1
• [3] Öngyújtó (Wikipédia), https://hu.wikipedia.org/wiki/%C3%96ngy%C3%BAjt%C3%B3
• [4] Bután (Wikipédia), https://en.wikipedia.org/wiki/Butane
• [5] How do you balance the equation C4H10+O2 = CO2+H2O?, https://socratic.org/questions/how-do-you-balance-the-equation-c4h10-o2-co2-h2o