Spoiler: A végén van valami olyan, ami eddig egyszer sem volt.

A Simcenter STAR-CCM+-szal többféle módon modellezhetjük a mozgó testeket. Ezen belül többféle kategóriát is létrehozhatunk. Az egyik kategorizálási mód az, hogy vannak az előírt forgó és transzlációs mozgások, illetve a 6 szabadságfokú mozgások. Utóbbi látható a következő ábrán.

Ebben a blogbejegyzésben nem a 6 szabadságfokú mozgásokkal, hanem az első kategóriából, azaz az előírt forgó és transzlációs mozgások kategóriájából a forgó mozgásokkal foglalkozom. Ebbe a kategóriába azok a forgómozgások tartoznak, amiknél előírom a forgási sebességet és azzal forog a rendszer, azaz az áramlási viszonyok sem nem gyorsítják, sem nem lassítják. Ezt a kategóriát is tovább lehet bontani csoportokra. Ez a csoport legyen az állandósult állapotban is használható megoldások és a csak időfüggő esetben használható megoldások.

Az első csoportba kétféle mozgásmodellezési módszer tartozik: a befagyasztott járókerék és a keverőfelület módszerek, azaz a Frozen Rotor és a Mixing-Plane módszerek. Ezek a módszerek időfüggő és állandósult állapotú szimulációk esetén is használhatók. A második kategóriába a csúszó háló módszert, azaz a Sliding Mesh módszert sorolom. Ez a módszer csak időfüggő esetben használható.

Mindegyik módszernek vannak előnyei és hátrányai a másik módszerekhez képest. Ezeket fogom röviden összeszedni ebben a bejegyzésben és egy (számomra fontos) szélturbina geometrián bemutatni. Azt, hogy melyik a legjobb módszer és melyiket kell használni, előre meg tudom mondani (illetve írni), hogy nem tudom. Feladat függően célszerű választani, mert vannak olyan esetek, amikor az egyik kell és vannak olyan esetek, amikor a másik használata a célszerűbb.

Egy ellenirányba forgó ikerturbina segítségével fogom a módszerek eredményeit összehasonlítása, de még előtte egy gyors kitekintés:

A Simcenter FLOEFD egy tökjó eszköz, szeretem használni, mert gyorsan és egyszerűen lehet benne szimulációkat készíteni. FLOEFD-n belül kell a forgó test és a forgó régió, viszont a tradicionális CFD-k esetén le kell modelleznünk az áramlási teret. Abból ki kell vonnunk a forgó régiót és a forgó régióból a forgó testet. A forgó testet ezek után kitörölhetjük a szerelésünkből, mert a kivágott felületen „fal” peremfeltételként definiáljuk majd ezt a testet.

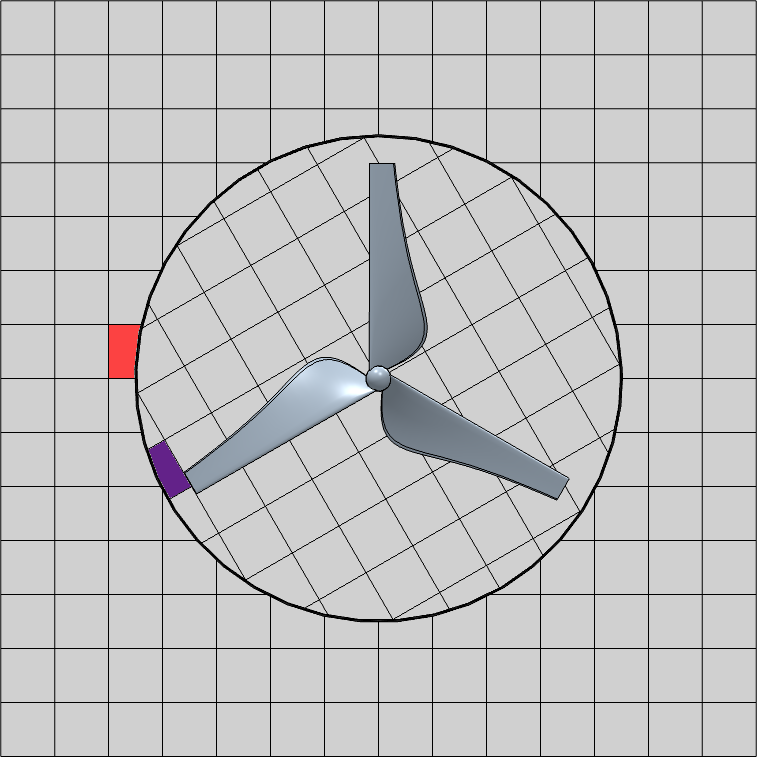
A következő ábrán egy szélturbina rotorja látható, ami a forgó test. A kerék körüli hengeres test a forgó régió, körülöttük a téglatest térfogat az álló rész (az egész modell a felénél félbe van vágva, hogy látszódjon a belseje). A Simcenter STAR-CCM+ egy hagyományos CFD-s gondolkodásmódot követő szoftver, azaz ezeket a testeket le kellett modellezni és ahogy a képen látható a forgó régióból a szélturbina rotorját kivágtam (a szimuláció során fal peremfeltétellel fogom modellezni, hogy ott a test). Ezek a CAD-es műveletek megoldhatóak Solid Edge-ben, NX-ben is, vagy a SC STAR-CCM+-on belüli CAD-es funkciókkal is, attól függően, hogy kinek mi esik kézre.

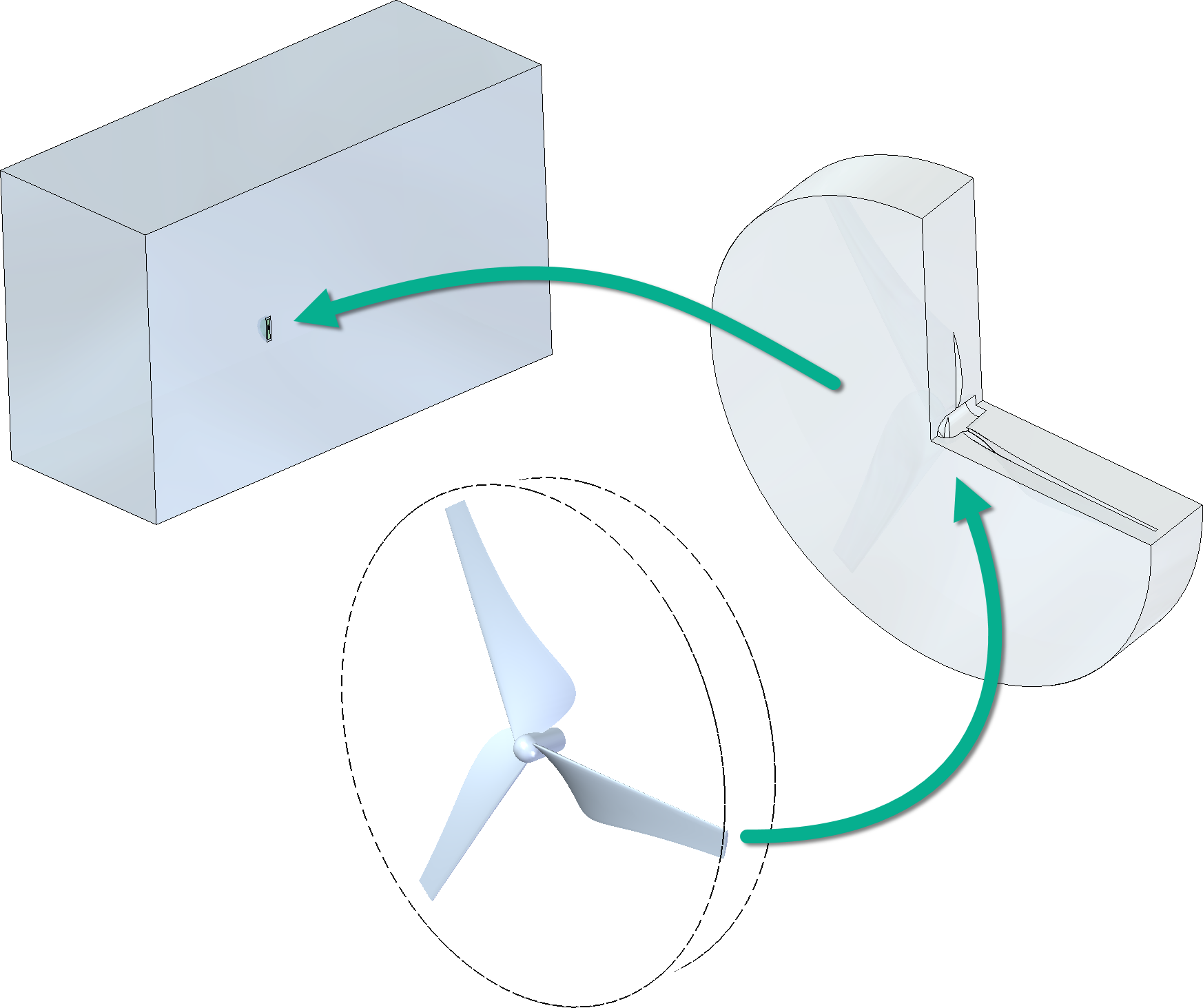
Frozen Rotor

Frozen Rotor módszer esetén a megoldás lehet időfüggő és állandósult állapotú. A módszer működését úgy a legkönnyebb elképzelni, hogy a forgó régióban a falon van egy mozgó fal peremfeltétel, ahol a fal omega x r sebességgel forog. A szimulációt lefuttatva a mozgó test a helyén marad, ez a szögsebesség csak annyit csinál, mintha forogna és azt a forgó sebességet rárakja. A módszer előnye a Mixing Plane módszerhez képest, hogy az örvényleválásokat a kiértékelés során meg tudjuk nézni. A módszer hátránya (igazából nem hátránya, hanem tulajdonsága), hogy ha van a környezetében valamilyen test, akkor a forgó mozgást egy adott állapotban modellezi, azaz a környező geometriák befolyásolhatják az eredményét. Utóbbi tulajdonság lehet előny is és hátrány is, azaz előnynek mondanám, hogy meg tudom nézni, hogy egy test 0°-os elfordulásnál, 60°-nál, 124,123°-nál és ahol szeretném, ott milyen áramlási kép alakul ki, és nem kell egy időfüggő szimulációt lefuttatni.

(Megj.: Az állandósult állapotú szimulációk gyorsabban lefutnak, viszont időbeli átlagolást tartalmaznak. Ha időfüggő szimulációt futtatok, akkor nincs időbeli átlagolás, viszont párszor körbe kell forgatom a kereket ahhoz, hogy kialakuljon az az áramlási kép, ami már hasonlít az állandósult állapotúra, és ezt csúszóhálós módszerrel kell megtennem, mivel a Frozen Rotor időfüggő esetben is egy helyben áll és egy helyben állva utánozza azt, hogy milyen lenne az áramlási kép, ha forogna és pont abban a pozícióban lenne). Ugyanez a tulajdonság (az, hogy a környezet visszahat a forgó régióra) lehet hátrány is, ha a lapáton integrális mennyiségeket akarok kiértékelni, mondjuk a rajta ébredő nyomatékot, akkor a több állapotot le kell futtatnom és azok értékeit átlagolnom kell egy táblázatkezelőben. További előnye az, hogy kevesebb számolási erőforrásigénye van, mint az csúszóhálós módszernek.

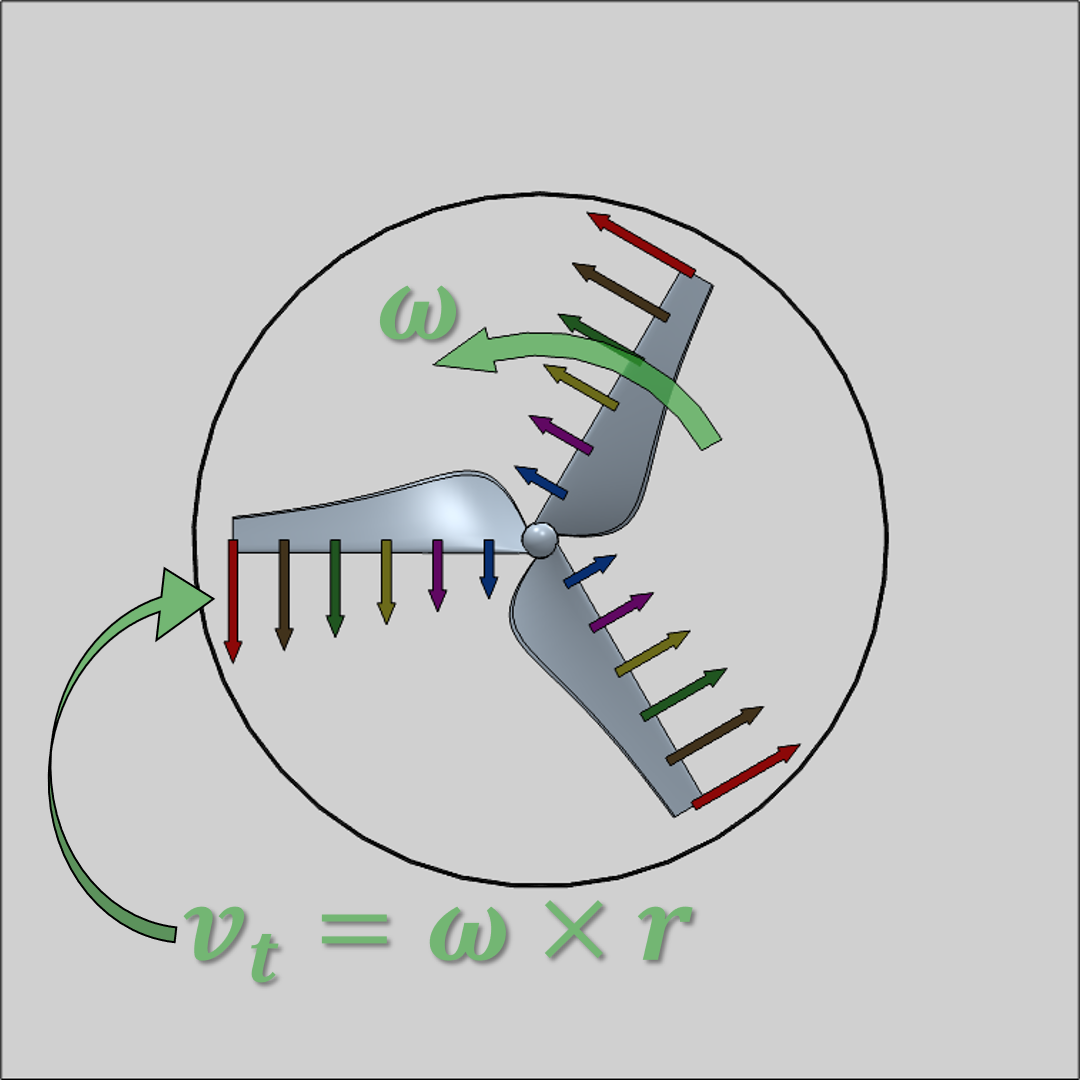
Frozen Rotor módszer megértését segítő ábra.

Mixing Plane

A Mixing Plane módszer egy időfüggő és állandósult állapotban is használható módszer. Számolási erőforrásigénye kedvezőbb, mint a csúszóhálós módszeré. Tulajdonsága, hogy nem egy adott állapotot modellez ez a módszer, hanem egy teljes körbefordulást. Ezt úgy teszi meg, hogy a forgó régióban a kialakuló áramlási viszonyokat körbeátlagolja. Ennek a módszernek a könnyebb megértését a következő egyszerűsített ábrák ismertetik. Itt azt még hozzá kell tennünk, hogy a szilárd testet is körbeátlagolja, azaz, ha a következő ábrát néztem akkor a forgási tengelyben a szilárd test aránya 100%, és ahogy megyek egyre kijjebb ez csökken annak függvényében, hogy radiálisan mekkora a szilárd testek aránya. Ez a szilárdtest átlagolás azt befolyásolja, hogy ahol 100%-ban szilárd test van, ott nem tud átáramolni a közeg, ahol 50% ott csak félig, ahol 0%, ott meg minden akadályozás nélkül.

Áramlási viszonyok az átlagolás előtt (Mixing Plane módszer megértését segítő egyszerűsített ábra)

Áramlási viszonyok az átlagolás után (Mixing Plane módszer megértését segítő ábra, elölnézet)

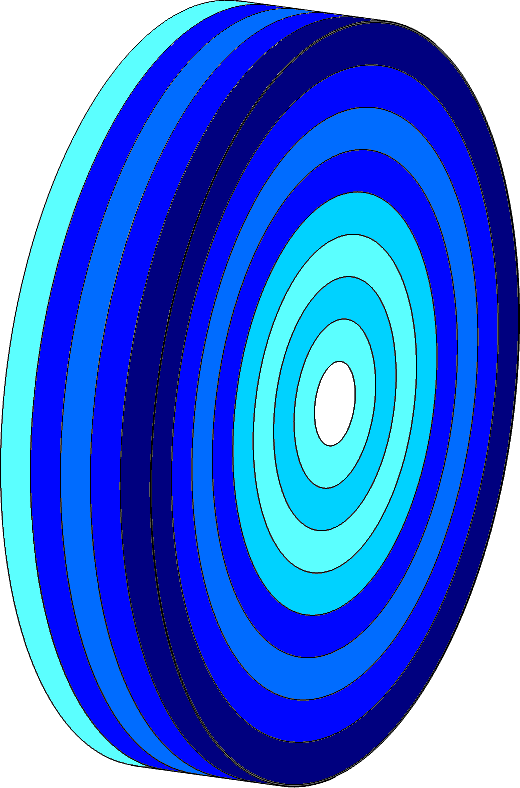
Az áramlási viszonyok az átlagolás után (Mixing Plane módszer megértését segítő ábra, oldalnézet, csak a forgó régió)

Az előző Mixing Plane-es módszernél a hengeres átlagolás felbontása nagymértékben függ a hálózástól!

Sliding Mesh

A harmadik, amit ismertetek ebben a blogbejegyzésben az a Sliding Mesh, azaz a csúszóháló módszer. Ez a módszer csak időfüggő szimulációk esetén érhető el. Ennek hátránya a nagyobb számolási erőforrásigény mely az időfüggő szimuláció tulajdonsága (azaz az, hogy az adott időpillanatban az áramlási viszonyok függnek az előtte lévő állapottól). Ez a módszer a háló régióját forgatja, ami azt jelenti, hogy a geometria (pontosabban a háló) is forog a megoldás során. Ha ezt a forgómozgást modellező módszert használjuk, akkor az örvényleválások (úgy ahogy a Frozen Rotor esetén is) modellezhetőek. Ennek a módszernek a könnyebb megértését a következő ábrák segítik: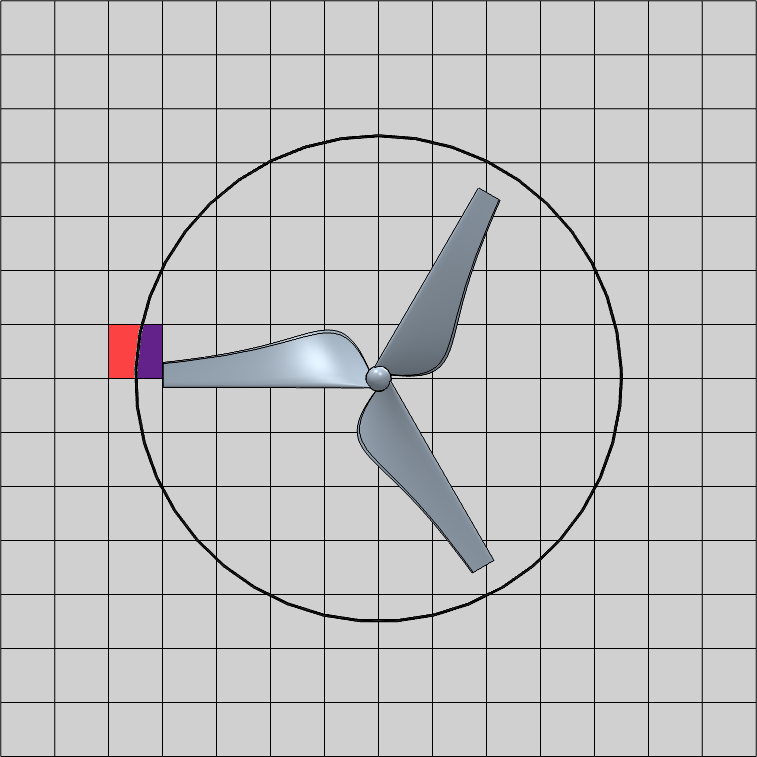

Geometria (régiók) helyzete t=0 sec időpillanatban (kiinduló állapot)

Pár időlépéssel később (t>0 sec)

Még egy gyors kitekintés:

Simcenter FLOEFD-ben ebből a három módszerből két módszer érhető el, a Mixing Plane és a Sliding Mesh.

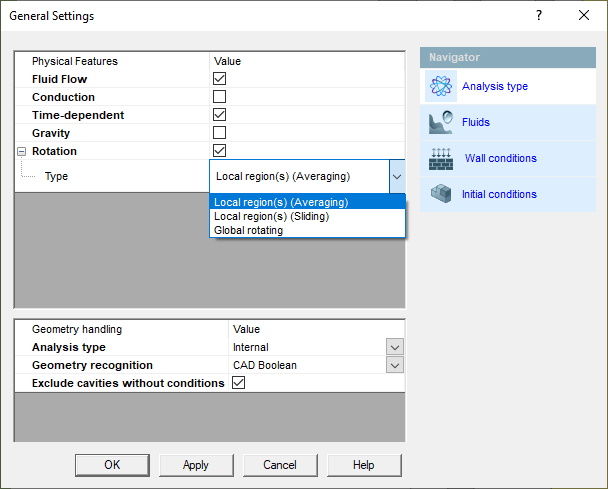
A Local region(s) (Averaging) a keverőfelület azaz a Mixing Plane-nek hívott módszer, míg a Local region(s) (Sliding) a csúszóhálós módszer. Ezeknek a módszereknek a nevei függnek attól, hogy a szoftver fejlesztője hogyan nevezte el őket. Mindegyik módszernek van 2-3 névvariációja, sajnos ezeket be kell azonosítani az általunk használt szoftverben.

Itt a blog közepén jegyezném meg, hogy amiket eddig írtam a blogban azoknak a dolgoknak van egy szakirodalma, illetve a következő dolgoknak is vannak olyan beállításai, amiket nem részletezek. A bejegyzés végén lévő hivatkozás tartalmazza ezekre a hiányosságokra a válaszokat és szakirodalmi hivatkozásokat.

Geometria

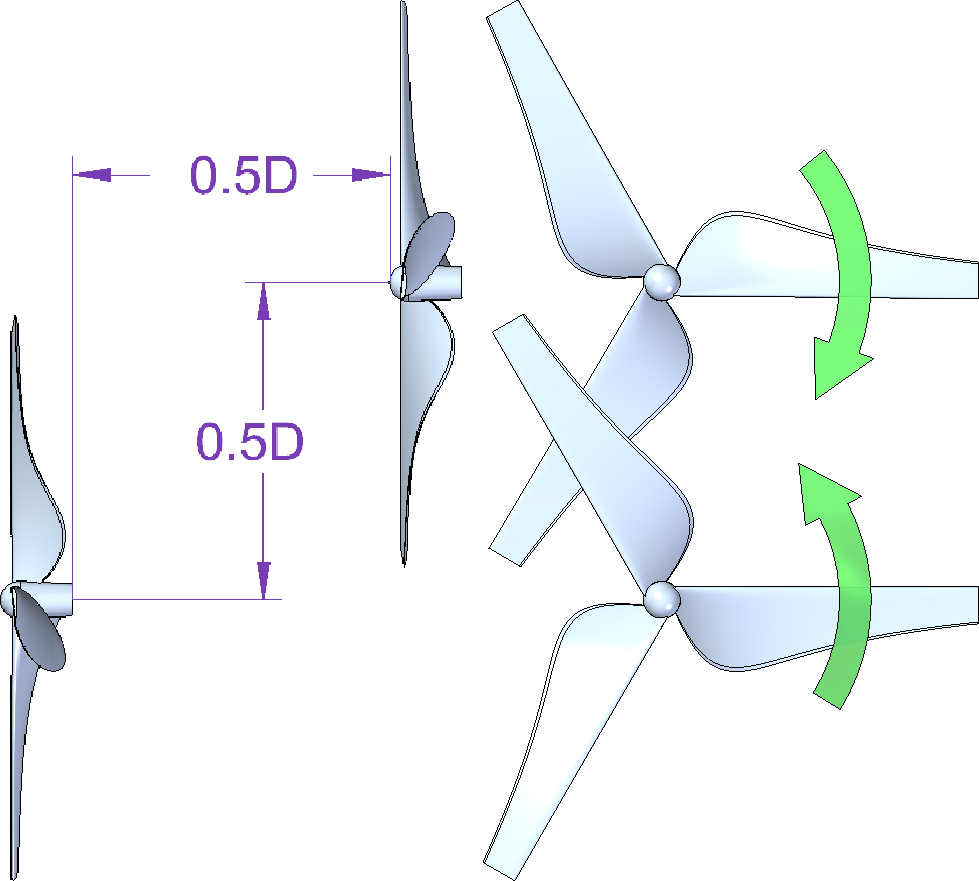
Nézzük akkor azt, hogy mivel fogjuk összehasonlítani ezeket a módszereket. A következő ábrán látható két rotor, ahol az első a hátsónak a tükörképe és egymással ellentétes irányba forognak. A két rotor egymástól fél-fél átmérőnyi távolságra van, ez jelen esetben 100-100 mm távolságra (igaz, ez az összehasonlításunk szempontjából most lényegtelen).

Szimulációs eredmények

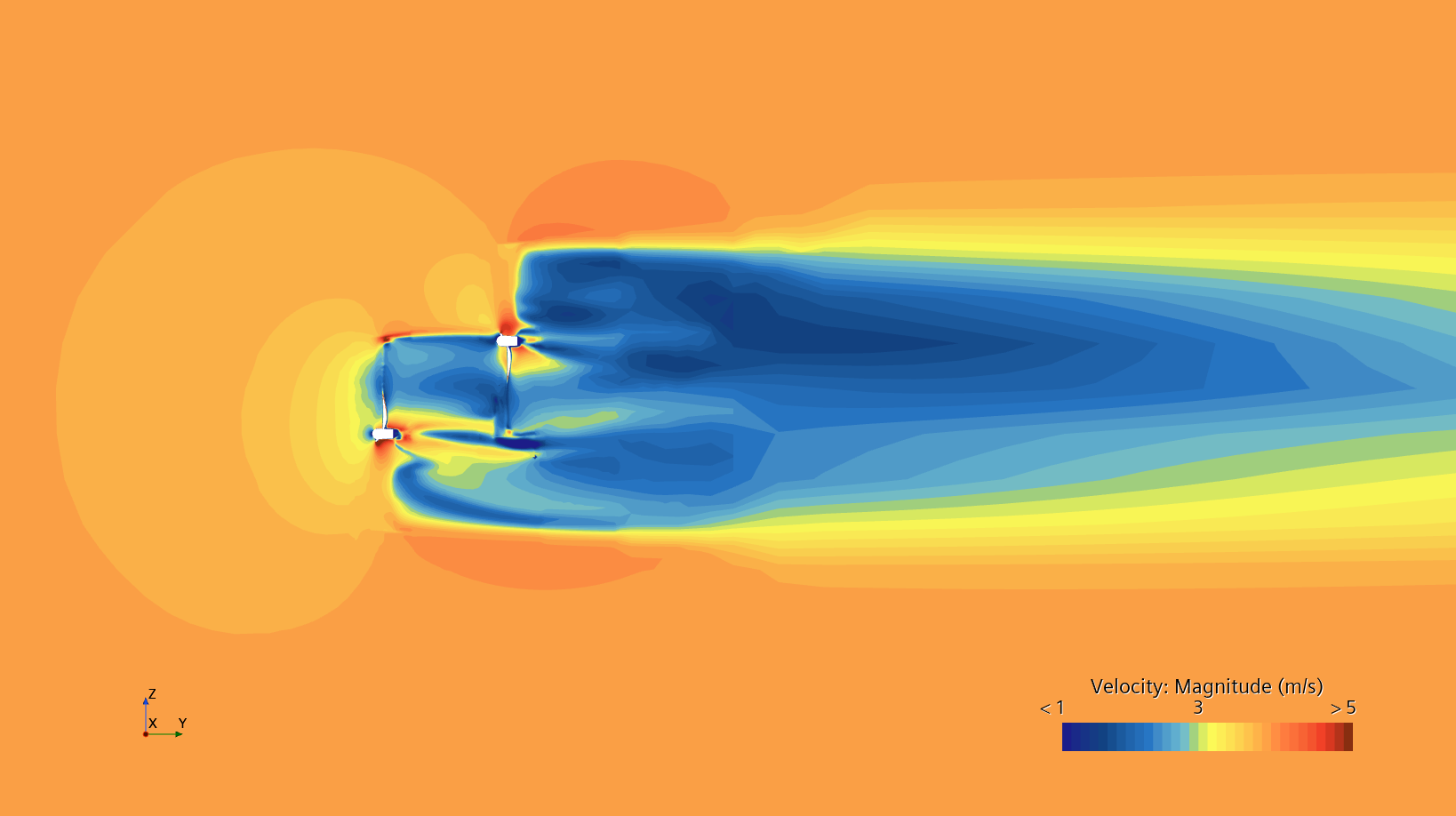
Ha lefuttatjuk a szimulációkat, akkor a középsíkban egy-egy síkmetszettel meg lehet jeleníteni áramlástani jellemzőket, pl. a sebességeket. Az egyik eset sebességmezője látható a következő képen. Az ábrán a turbinák környezetét látjuk, nem a teljes áramlási teret. Megfigyelhetjük, hogy a beáramló közeg a rotorokba ütközve lelassul és a kerekek mögött kialakul egy leválási régió. Az, hogy a közeg lassul a turbinák mögött, azt jelenti, hogy energiát vett ki belőle. Ha gyorsulna a közeg a lapátok mögött, akkor az azt jelentené, hogy egy ventilátorunk van…

A síkmetszeteknél látványosabb az, ha az eredményeket térben ábrázoljuk.

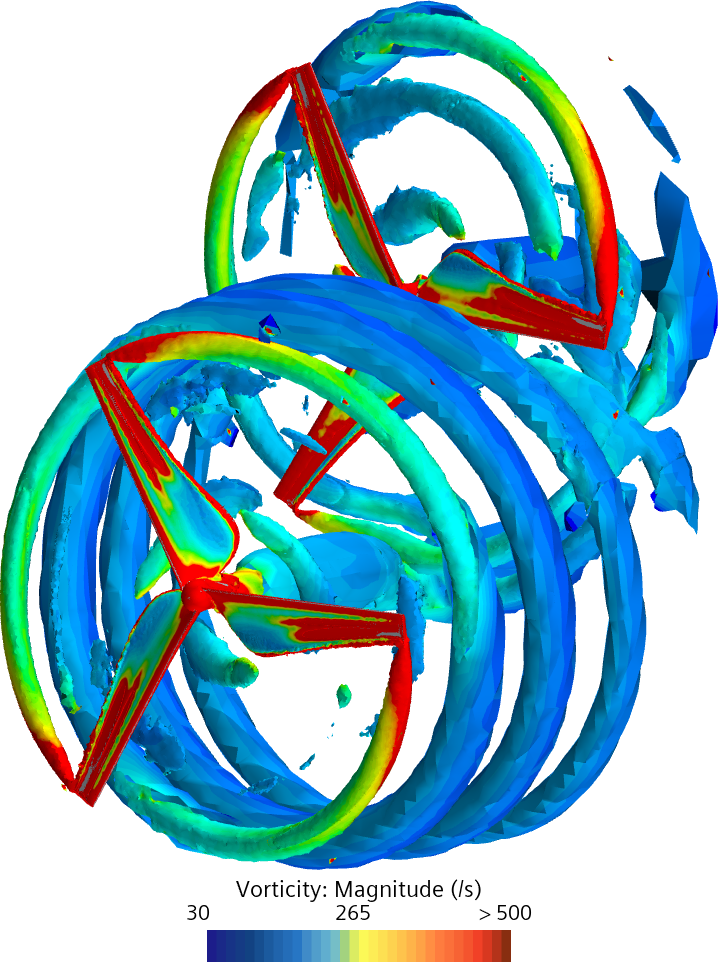
Időfüggő eset (csúszóháló módszer), 6 körbefordulás után (örvényesség a Q kritérium Q = 800 felületen ábrázolva)

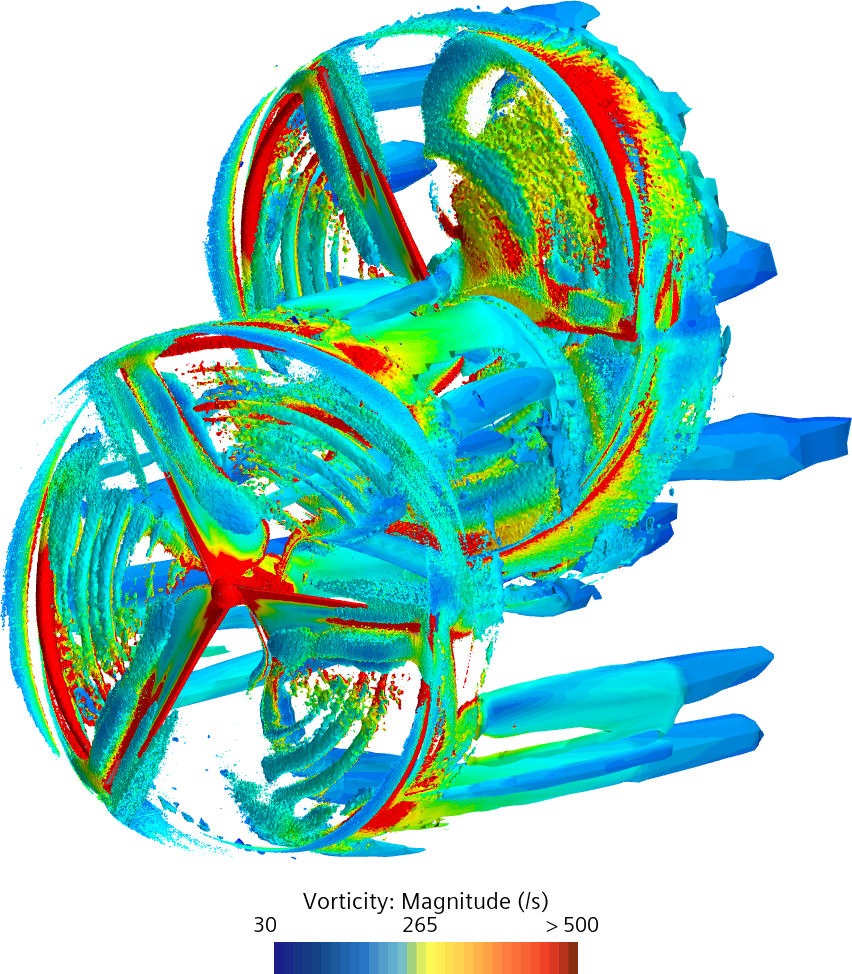
Állandósult állapot Frozen Rotor módszerrel (örvényesség a Q kritérium Q = 800 felületen ábrázolva)

Állandósult állapot Mixing Plane módszerrel (örvényesség a Q kritérium Q = 800 felületen ábrázolva)

Az előző ábrák a turbina közvetlen környezetében mutatják meg az örvényességet, míg a következő ábrákon egy kicsit nagyobb távolságból látjuk az áramlási képet.

Időfüggő eset (csúszóháló módszer), 6 körbefordulás után

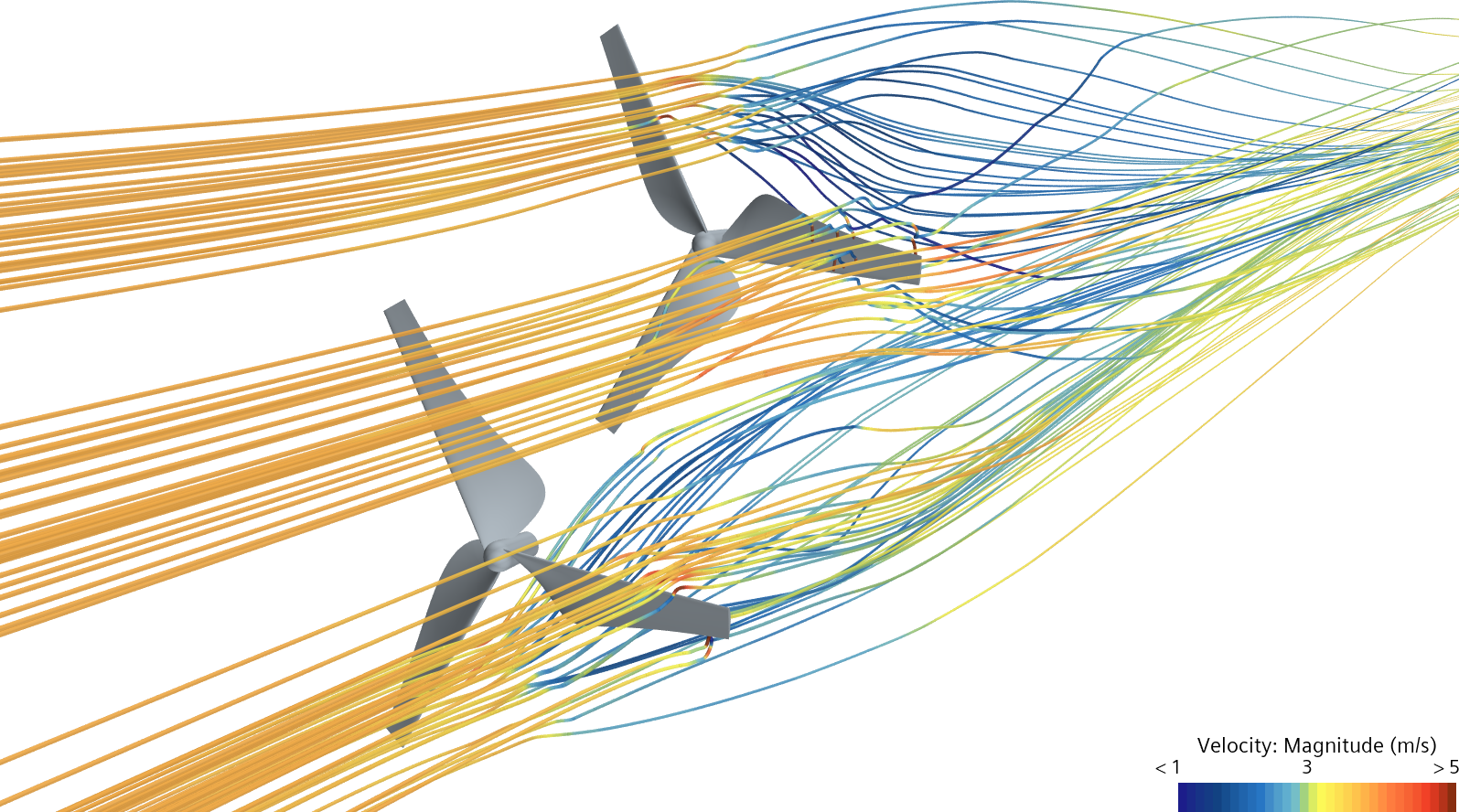
Állandósult állapot Frozen Rotor módszerrel

Állandósult állapot Mixing Plane módszerrel

Az előző ábrákon azt láthatjuk, hogy az időfüggő esetben az áramlás a turbina mögött is csavarodik. Ugyanígy egy bizonyos fokú örvényesség megfigyelhető a Frozen Rotor módszeres ábrán is. A Mixing Plane módszerrel futtatott szimuláción az áramlási kép jóval kevésbé mutat örvényesen kavargó közeget. Utóbbi esetén (mivel ez egy átlagolt módszer) ott is örvényesebben lép ki a közeg a forgó régióból, ahol nincs lapát (mivel ott a körbefordulás átlaga okozza az örvényt).

Frozen Rotor esetén az az örvényesség a lapátról indul, viszont ezen is látszódik az állandósult állapot miatti összes „időlépés átlaga” hatás. Így az eredmény „szét van maszatolva” az áramlási térben és a forgó régióból kilépő közeg „egyenesen” örvényes. Időfüggő esetben, aminél semmilyen időbeni átlagolás nincs, a lapátvégről induló örvények az áramlási térben futnak végig, addig míg el nem disszipálódnak vagy bele nem ütköznek a második turbinába. Ugyanitt az időfüggő esetnél a második turbina örvényessége kisebb, mint az elsőé (valószínűleg azért, mert lassabb az odaérkező szél).

Az áramlási képek olyanok, amilyenek a módszerből adódnak. Egyik sem jobb, egyik sem rosszabb, mint a másik, hanem olyanok amilyennek lenniük kell az adott módszer szerint.

Nézzük a nyomatékokat. Azt tudom a szimulációk lefuttatása nélkül is, hogy ha nincs semmi a test környezetében, azaz egy üres térbe rakok be egy darab rotort, akkor mind a három módszer azonos (vagy közel azonos) eredményt ad. Abban az esetben, ha valamilyen egyéb testet belerakok az áramlási térbe, akkor a módszerek eltérő eredményeket adhatnak attól függően, hogy az adott pozícióhoz milyen hatást-visszahatást generál a forgó testre a környezet. A következő ábrán az első és a hátsó rotor nyomatékai láthatóak.

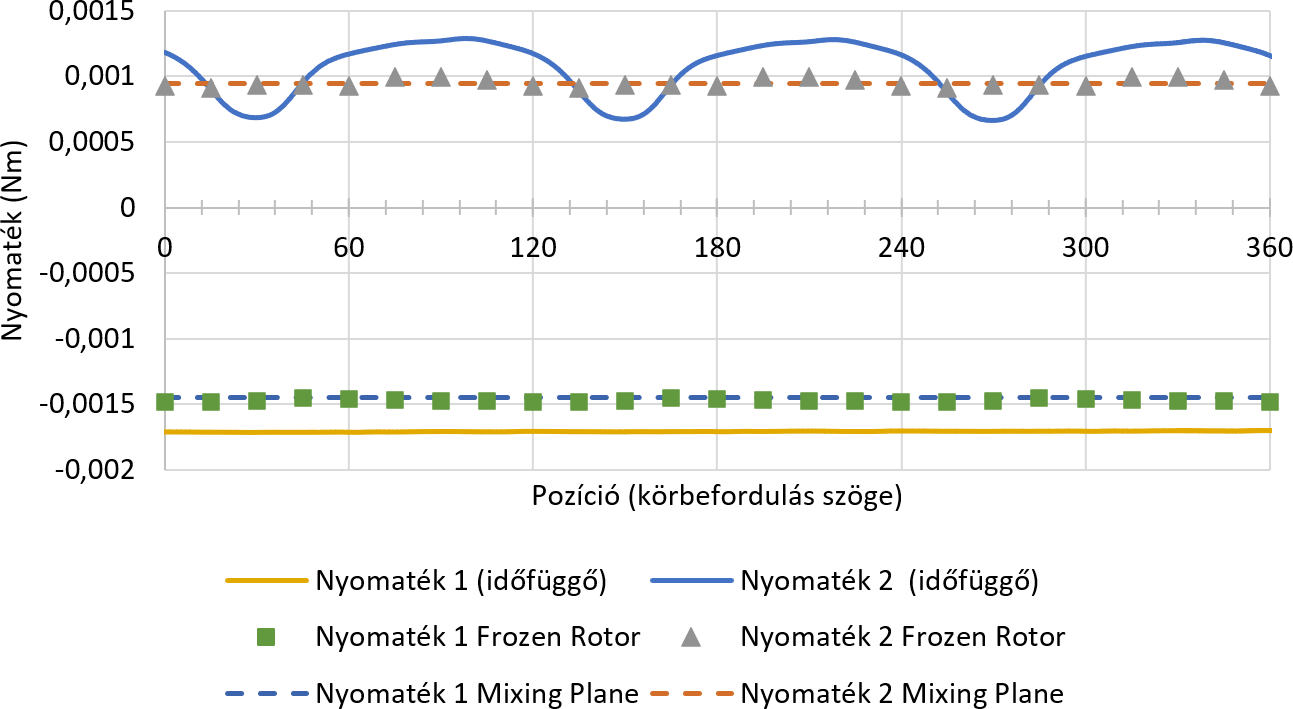
Az ábrát megvizsgálva megállapíthatjuk, hogy az adott pozícióban nincs, vagy csak csekély a visszahatása az első kerékre (ezek a Nyomaték 1-ek). A hátsó keréknek (ezek a Nyomaték 2-k) az első kerék hatása látszódik. Ezt onnan látom, hogy az első kerék nyomatékai nem változnak egy körbefordulás alatt. Amennyiben változnak, akkor ebben a nagyításban azt nem lehet szemmel észrevenni. A hátsó keréken viszont változnak a nyomatékok. Ez leginkább a kék folytonos vonallal ábrázolt időfüggő esetben látható. Állandósult állapot esetén van egy kisebb kilengése a Frozen Rotoros eredménynek, de az meglátásom szerint elhanyagolható. Az eredmények előjelei eltérnek, ennek oka az, hogy ellentétes irányba forogtak.

Mixing Plane esetén egy értéke van a szimulációnak, mert az minden egyes geometriai helyzetben azonos eredményt produkál. Frozen Rotor esetén a geometria pozíciójának van jelentősége, így 15-15°-kal elforgattuk a rotorokat és úgy futtattunk több szimulációt. A befagyasztott járókerekes szimuláció eredményei alapján megállapítottuk, hogy a forgó test és a környezet interakciója jelen esetben elhanyagolható.

Az eredményekből az látszódik még, hogy hiába vártuk volna az időfüggő esethez hasonló görbét a Frozen Rotor esetén, azt nem kaptuk vissza. Ennek az oka feltételezhetően az, hogy az állandósult állapotú szimuláció az időben átlagolt (elméletileg benne van az összes időpillanat átlaga), és az az örvény, ami a lapát végéről indul valószínűleg ily módon kiátlagolódott a megoldás során.

Másik tapasztalatunk az volt, hogy az állandósult állapotú esetek közel azonos eredményt adtak. Azaz az összes Frozen Rotoros szimuláció nyomatékának veszem az átlagát, az a Mixing Plane nyomatékának az értékét adja. Ebből arra következtettünk, hogy amíg két kerék van csak a szimulációban és nincs ott az oszlop, a gondola vagy a talaj addig elég csak egy esetet lefuttatni a Frozen Rotor-ral és nem kell adott szögenként külön-külön lefuttatni a szimulációt mert nem nyerünk semmi extra nyomatékértéket a sok szimulációval. Az az egy szimuláció viszont lehet a Mixing Plane-es is, nem kell, hogy a Frozen Rotor-os szimuláció legyen.

Számolási erőforrásigények

A CFD szimuláció egy iteratív megoldás, aminek a futtatása közben néztük a számolási erőforrásigényt is. Ez azért jó nekünk, mert így, ha úgyis ugyanazt az eredményt adja a két állandósult állapotú megoldás, akkor azt célszerű lefuttatni, ami gyorsabban fut, illetve azt, ami kevesebb memóriát igényel. Az első 500 iteráció memóriafelhasználása és számolási ideje a következő ábrán látható.

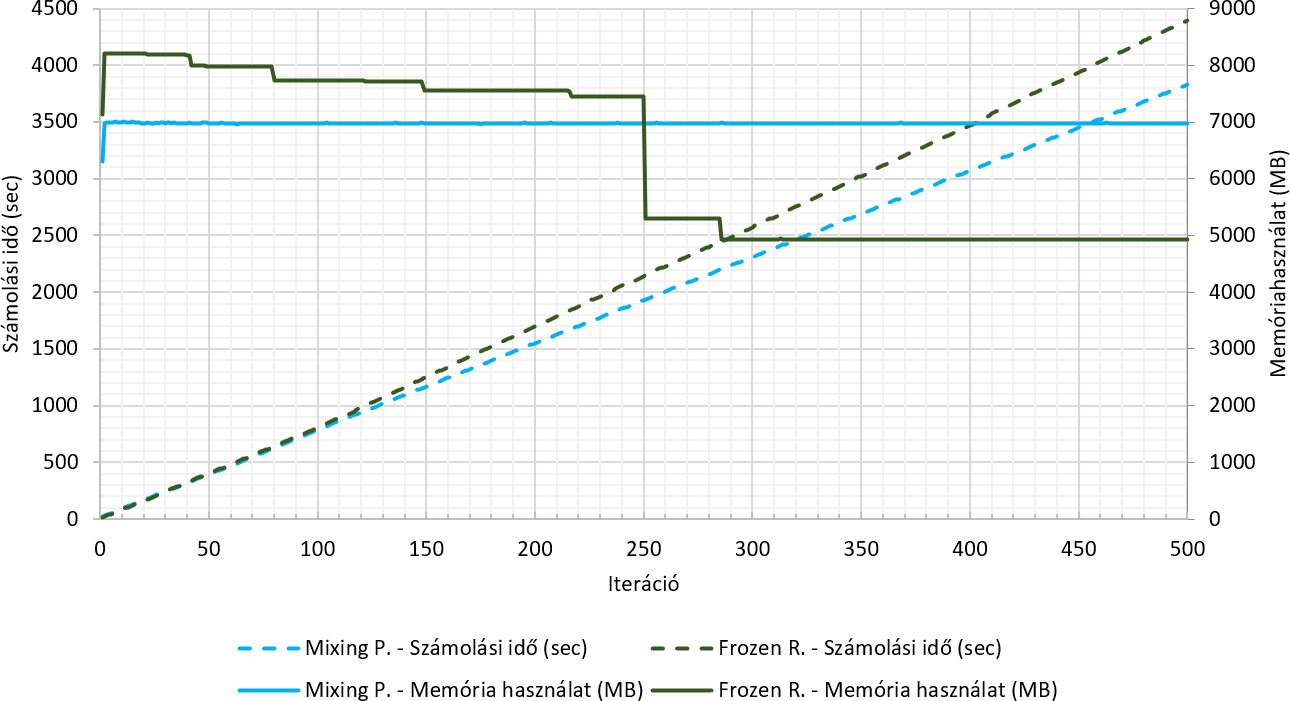
Ezek az eredmények azt mutatják, hogy a Mixing Plane módszer kevesebb ideig számolt, azaz egy darab iterációhoz kevesebb CPU-t használ, mint a Frozen Rotor-os megoldás. Számolási idő szempontjából, ha van bőven memóriánk és a processzorral állunk szűkén, akkor ezt a módszert célszerű választani.

Ha a memóriahasználatot nézem, abban az esetben a Mixing Plane módszer egy közel konstans memóriaigénnyel rendelkezik. Míg a Frozen Rotor módszer egy nagyobb memóriaigénnyel indít, majd lépcsősen csökkenve beáll egy fix értékre. A Frozen Rotor kezdeti memóriaigénye nagyobb, mint a Mixing Plane-é, viszont miután beállt az áramlás egy adott szintre, utána lecsökkent a Mixing Plane módszer memóriaszükséglete alá.

Fontos továbbá azt is megjegyezni, hogy ezek az erőforrásigények az én adott szimulációmra vonatkoznak. Azonos elemszám esetén, ha mást vizsgálnék (pl. szivattyú, autó kerék…) akkor a memóriafelhasználás és a számolási idő is eltérhet módszerenként. Azaz az eltérésük aránya nem fix, viszont feltételezhetően a kisebb/nagyobb viszony fennmarad.

Ezt a szimulációt Simcenter STAR-CCM+ 2022.1-ben futtattam le. Minden új verzió tartalmaz valamilyen újítást, így előfordulhat, hogy gyorsabb iterációk, optimalizált memóriafelhasználás vagy egy ráncfelvarrott funkció belekerül/belekerült egy újabb verzióba.

 

Záró gondolatként meg szeretném jegyezni, hogy Témavezetőm azt mondta egyszer, hogy szerinte az emberiséget a lustaság hajtja előre. Azaz azon gondolkozunk, hogy hogyan kellene kevesebbet dolgozni úgy, hogy elvégezzük az adott feladatot. Ezt azért gondoltam megjegyezni itt a blog végén, mert ez a blogbejegyzés nagymértékben támaszkodott az Applied Sciences folyóirat Advances and Applications of CFD (Computational Fluid Dynamics) különszámában megjelent egyik cikkére, a Comparison of Mixing Plane, Frozen Rotor, and Sliding Mesh Methods on a Counter-Rotating Dual-Rotor Wind Turbine-ra (szerzők: Szlivka F., Hetyei Cs., Fekete G. és Molnár I., a cikk további adatai Applied Sciences, vol. 13, no. 15, p. 8982, Aug. 2023, DOI: 10.3390/app13158982. Elérhető itt vagy itt). Minden olyan hivatkozás, ami szükséges lenne az itteni állítások alátámasztásához, megtalálható – reményeim szerint – ebben a cikkben.

 

Kérdőív

Kedves Blog olvasónk!

Köszönöm, hogy elolvastad ezt a blogot (vagy legalábbis lepörgettél idáig és megakadt a szemed ezen a soron). Ez a blog más, mint a többi és teszt jelleggel készült. Régebben is voltak ilyesmi próbálkozásaim (ld. Kellően sűrű a hálóm sorozat) a nézzük meg a színes ábra blogok mellett (pl. Kávéfőzés Solid Edge-el vagy Öngyújtóval tűzgyújtás).

Olyan nagy kéréssel fordulok most felétek, hogy személyesen (pl. az EPLM Trends 2023 konferenciánkon), vagy a lenti kérdőív segítségével jelezzetek arról vissza, hogy milyen jellegű szimulációs blogból látnátok többet. Legyen több ilyen bejegyzés ami eddig a Tudásbázisunkba került, vagy legyen több 10+1 lista, vagy valamilyen színes, bulváros téma vagy koncentráljunk jobban az ügyfeleinkre és kérjük meg őket, hogy írjanak ők egy blogbejegyzést arról, hogy mit csinálnak/csináltak éppen.

Ha a beágyazott kérdőív nem működne, a kérdőív elérhető ezen a LINKEN is.

Köszönöm szépen a kitöltést!