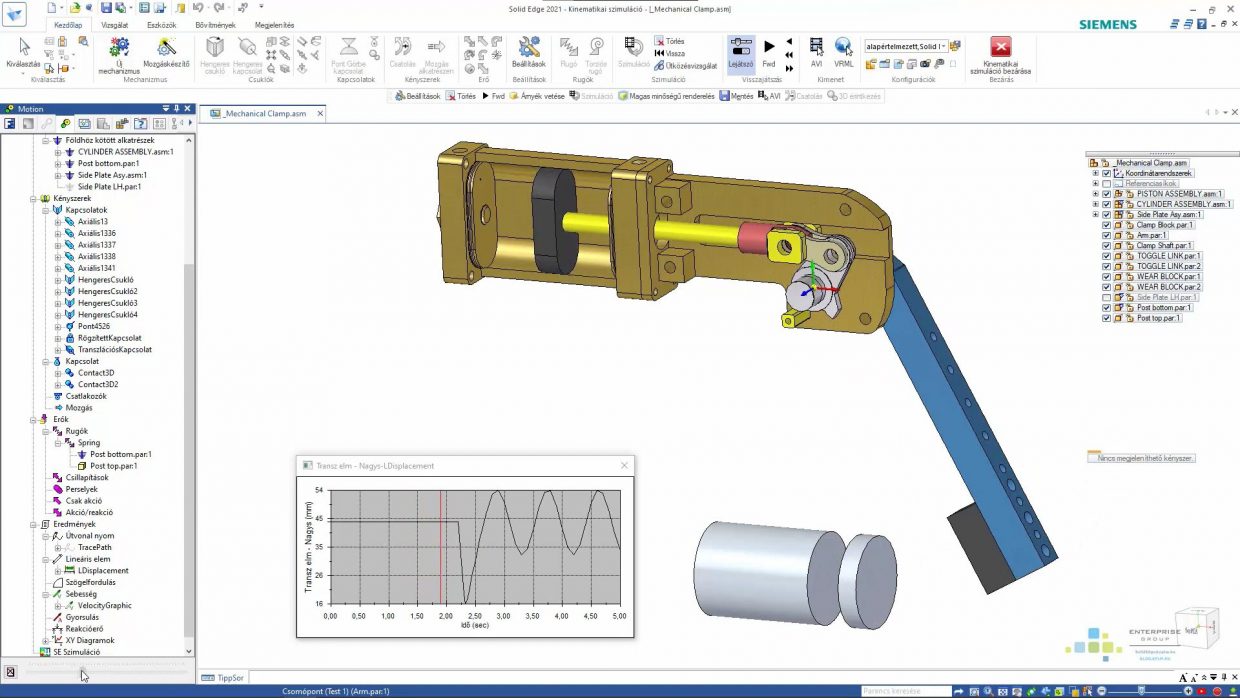
Kellően sűrű a hálóm? VI. – Időlépés meghatározása Solid Edge Motion-ben
Most, hogy megvagyok a végeselemes és az áramlástanos szimulációk hálózásával és az eredmények kiértékelésével, végre eljutottam a Motion-höz (bízom benne, hogy nem csak én, hanem más is elolvassa és akkor eljutottunk a helyes ragozás 😊).
Az első három bejegyzésben a Solid Edge Simulation hálózásával foglalkoztam és a hálófüggetlenségi vizsgálattal, aztán a FLOEFD-vel, és annak a „kézi” és az adaptív hálózójával. Eddig mindig volt egy szilárd test és azt hálóztam, vagy az azt körülvevő teret, most a mozgástani szimulációs modult fogom bemutatni, ahol a háló nem egy „kézzel fogható” dolog, hanem az idő. Az idő alatt a szimuláció (fizikai) idejét értem, azaz, ha egy folyamat 5 másodpercig tart, akkor azt az 5 másodpercet bontjuk itt fel apró időlépésekre és azokkal nézzük meg a folyamatot.
Szóval akkor ebben a bejegyzésben a Solid Edge Motion lesz, amihez a 2020-as Trends-en bemutatott modellt fogom használni. Akinek fel van telepítve Solid Edge-e, nekik a modell a C:\Program Files\Siemens\Solid Edge [évszám]\Training\Load Transfer útvonalon érhető el.
A következő videóban az látható, amire a Trends-es videóban nem volt idő, azaz lépésről lépésre a feladat megoldása.
A videóban lefuttattam ugyanazt a szimulációt háromszor. Mindegyik esetben a szimuláció 5 másodpercig tartott, viszont egyszer 10, egyszer 50 és egyszer 500 képkockát tartalmazott a szimuláció. Amennyiben lineáris eloszlást feltételezünk, akkor az első esetben 0,5 másodpercenként, a másodikban 0,1 másodpercenként és a harmadik esetben 0,01 másodpercenként számolt egyet a szoftver.
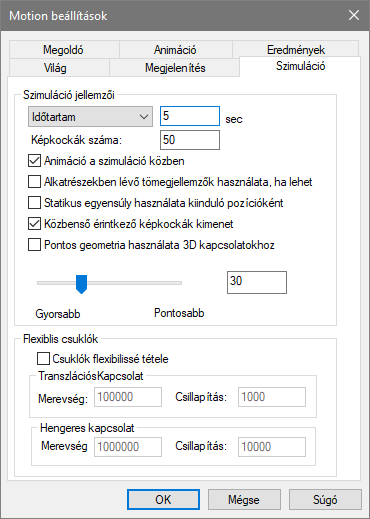
Az eredményeken látszódott, illetve a kimentett eredményeken is látszik, hogy ez a lépésköz csak egy javaslat, ahol tudja tartani a szoftver ott tartja, viszont, ha úgy jön ki a matek, akkor kisebb lépésekkel is számol. Ilyen például a következő képen látható csúcsok.
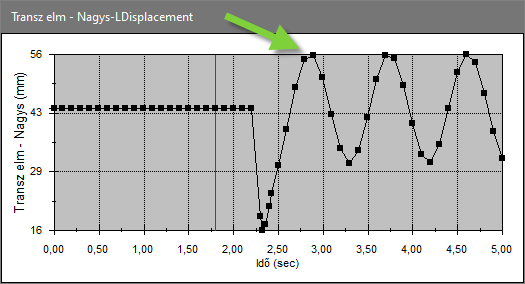
Ennek az oka az, hogy a Solid Edge Motion az időlépéseket kiiterálja. Ha valamelyik időlépésnél túl nagy az iterációs hiba, akkor azt a lépést törli és helyette egy kisebb időlépéssel számol.
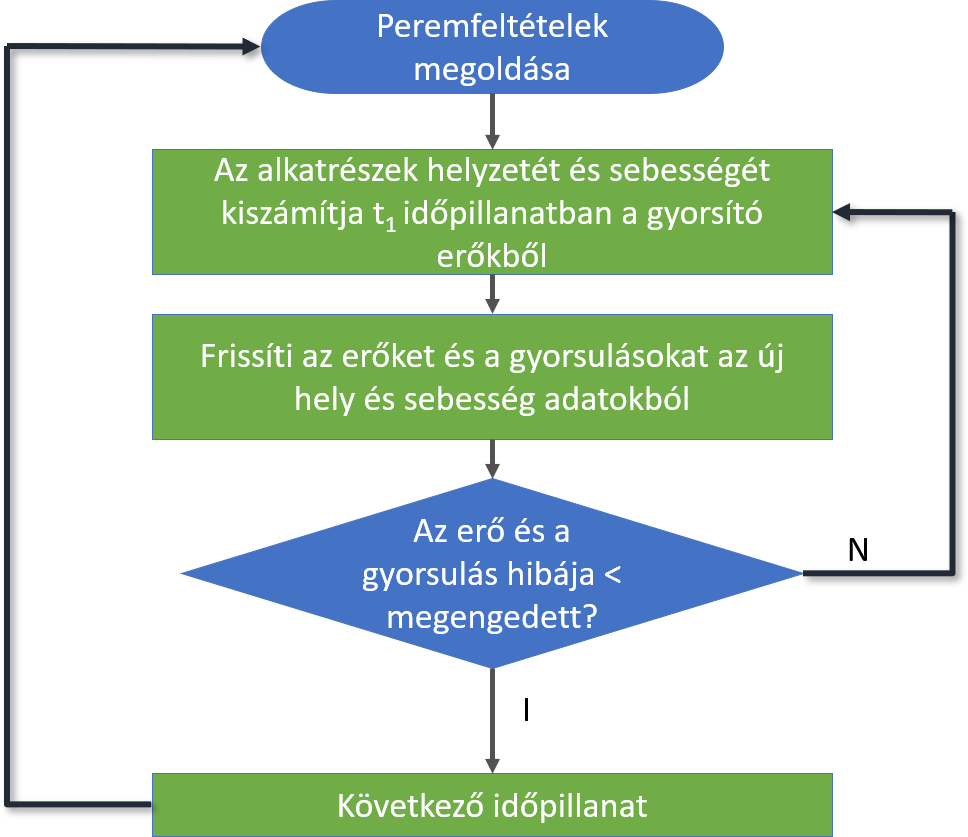
A videóba megmutatom, hogy ezt hol lehet állítani, de nem nagyon térek ki rá. Ez az ablak a Motion beállításain belül a Megoldó fülön található.
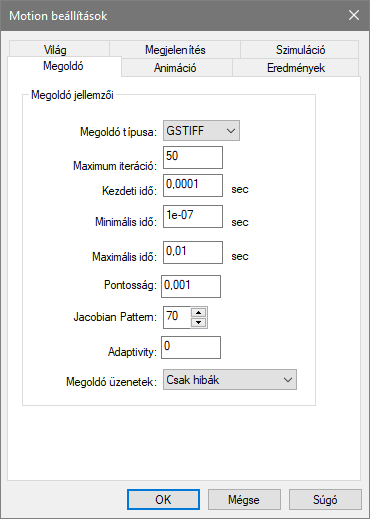
Tapasztalatom szerint az előző ablakban nagyon nagy ütközések és kontaktok esetén a maximum iterációt célszerű itt állítani, illetve a megoldó típusát.
A megoldók nevei ránézésre semmit mondók, van GSTIFF meg WSTIFF és SI2 GSTIFF…
A GSTIFF név onnan származik, hogy Gear változó lépésű integrációs módszert dolgozott ki merev differenciálegyenletek megoldására. A WSTIFF Wielenga módszerét használja. Az SI2 GSTIFF a GSTIFF egyik átirata, ahol más stabilitási módszert használnak (SI2=Stabilty Index 2).
A megoldókról röviden annyit célszerű tudni, hogy a
GSTIFF
- az alap megoldó,
- az elmozdulásokat számolja ki, onnan származtatja a többi jellemzőt,
- gyorsabb, mint a többi megoldó,
- az esetek döntő többségére jó és ezt célszerű használni (mert gyors és kellően pontos).
WSTIFF
- szakaszosan ható erőkhöz és mozgásokhoz ajánlott (pl. két hullámos felület egymáson csúszása esetén a kontakt erők ilyen szakaszosan ható erőnek számítanak, oszcilláció mozgásokhoz…),
- véletlenszerű lépésköz változásokat jobban lekezeli, mint a GSTIFF,
- mivel jobban kezeli a véletlen időlépéseket így, ha valami ütközik, csúszik vagy valamilyen egyéb okból kisebb időlépéssel kell vizsgálni a szimulációt pontosabb megoldó, mint a GSTIFF,
- lassabb, mint a GSTIFF.
SI2 GSTIFF
- sebességekhez és gyorsuláshoz pontosabbak,
- kisebb lépésközök javasoltak, mint a sima GSTIFF vagy WSTIFF megoldó esetén,
- lényegesen lassabb,
- azokhoz a szimulációkhoz javasolt, ahol a gyorsulás számottevő (pl. nagy frekvenciás oszcilláló mozgás).
Megjegyzés: Ebben az ablakban a pontosság a megoldóra vonatkozik, amennyiben a geometria lekövetését szeretnénk állítani, azt a Szimulációs fülön tudjuk megtenni. Két beállítás van itt erre, az egyik egy csúszka a másik a Pontos geometria használata 3D kapcsolatokhoz. A Pontos geometria… checkbox a CAD geometriához egy nagyon közel álló testet, míg a csúszka ehhez képest egy jobban egyszerűsített geometriát használ. (Bármelyiket is választom, a szimulációban lévő geometria nem lesz olyan pontos, mint a CAD geometria.) Ezt próbáltam meg ábrázolni a következő képen.
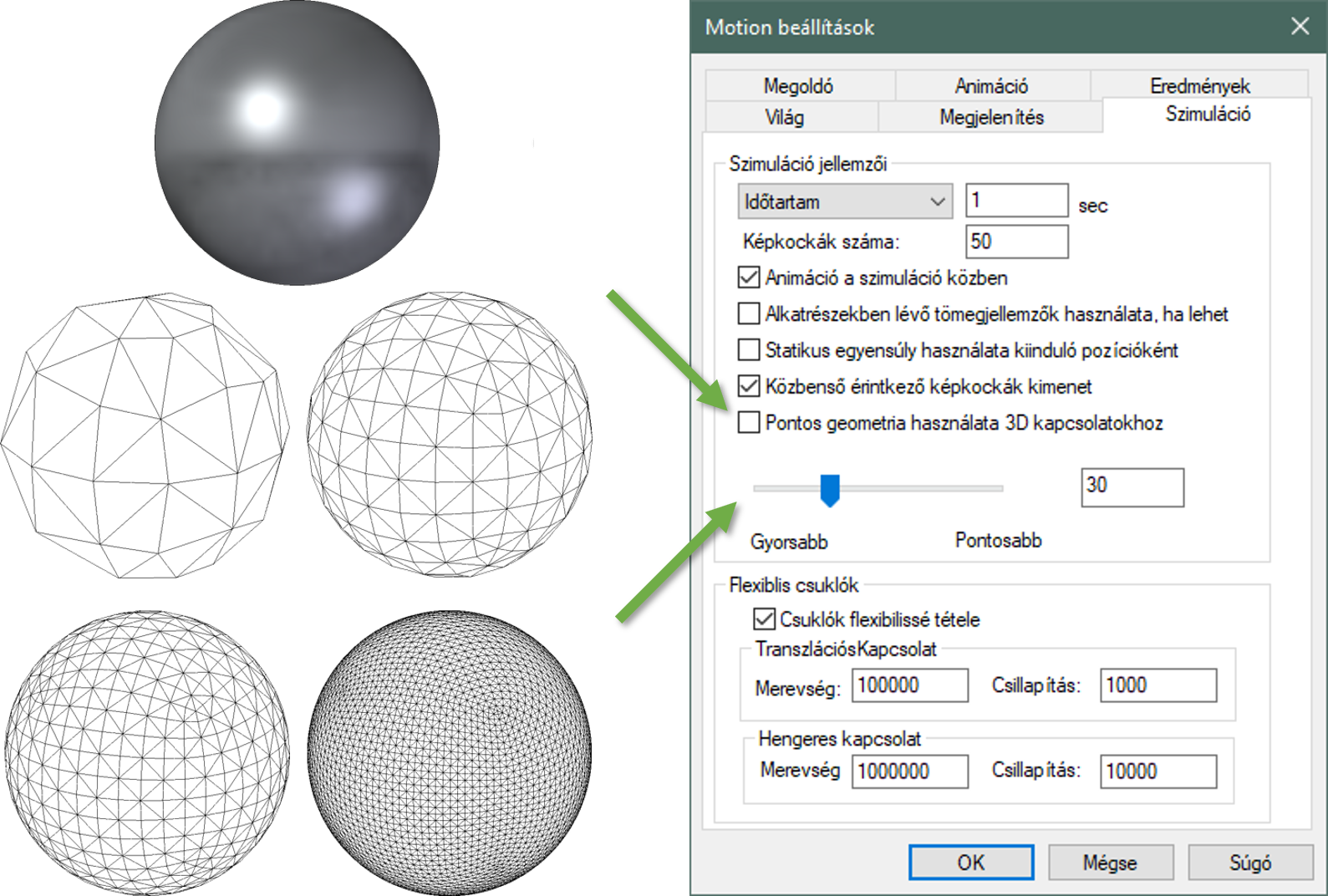
Visszatérve a kiindulási feladatra, lefuttattam ugyanazt a szimulációt ugyanazokkal a beállításokkal 10, 50 és 500 képkockával. Ha átrakom ezeket az eredményeket egy táblázatkezelőbe és ott görbét illesztek az elmozdulásokra, akkor a következőt kapom:
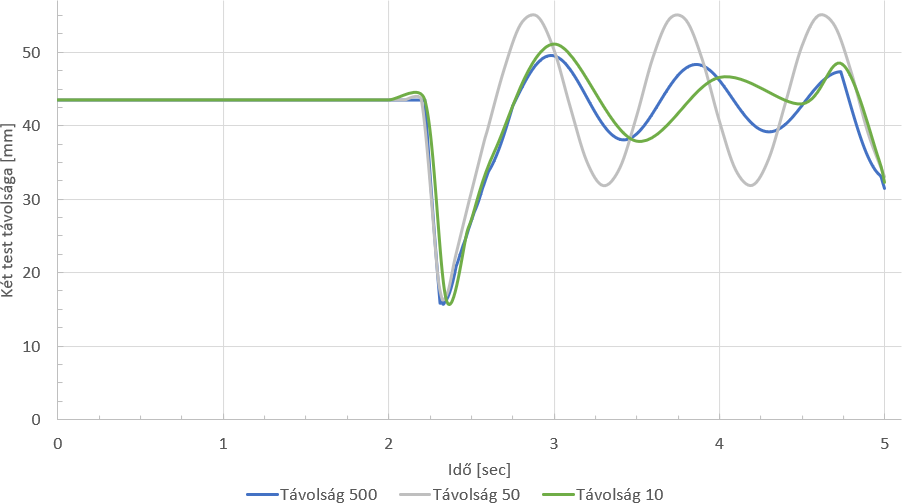
Az előző ábrán mivel görbét illesztettem a szimuláció eredményeire, így nagyon szépek lettek a szinuszos hullámok. Az előző ábrával az a baj, hogy az eredményeim nem ilyen részletesek, így vonalakkal összeköve jobban látszódik a szimuláció pontossága, illetve a szimulált eredmények.
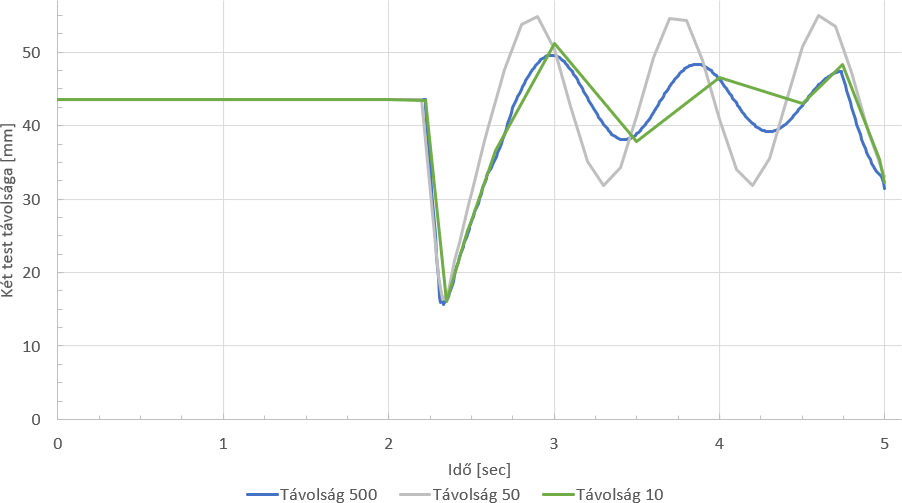
A két ábrát összehasonlítva azt látom, hogy az ütközés előtt nincs ott az a felugrás, azaz spontán nem ment előre a kis henger azelőtt, hogy a nagy neki ment volna (JPÉ szerint, ez nem is lehet, mert ott volt előtte a másik henger).
A két ábra megegyezik abban, hogy amíg nem ütközött a két test, addig az állandó méretű volt a két test közötti távolság, azaz ugyanabból a pozícióból indult ki a szimuláció.
Mindkét ábrán megfigyelhető, hogy a 2,3-2,35 másodperc környékén lévő ütközés ideje kicsit eltér. Ezt úgy valószínűsítem, hogy az időlépés miatt egyszer kicsit a valós ütközés elé egyszer egy kicsit a valós ütközés utánra iterálta ki a megoldó az ütközést.
Azt látom a Távolság 10 esetén, hogy ami a görbés megjelenítésnél szinusz vagy szinusz szerű hullám volt, az a vonalas ábrán látszódik, hogy nem az.
Azt látom a Távolság 50 esetén, hogy az az ütközés, ami az Távolság 10 és az Távolság 500 esetén is előjött (4,745 másodpercnél) az itt nem jött elő. Azt feltételezem, hogy mivel más időpillanatokban számolt a szoftver, valószínűleg máshogy adódtak ki a sebességek és így jött ki ebben az esetben a pozíció.
Ezek a feltételezések úgy gondolom, hogy hasznosak, mert ezekkel és a harmadik blogbejegyzésben írt módszerrel a 2,3 és a 2,35 közötti ütközés pillanatát ki lehet iterálni, azaz, ha írom az időpontokat és csökkentem az időlépés nagyságát, ha a két egymást követő eset közötti különbség egy adott szint alá csökken akkor az az eredmény háló khömm… akarom írni időlépés független. Jelen esetben 10-ről 50-re 1,08% a különbség, míg 50-ről 500-ra 0,62% az előző időpillanathoz képest (az ütközés az első esetben 2,352460259 sec-nél, a másodiknál 2,327236942 sec-nél és a harmadik esetben 2,312997478 sec-nél következett be).
Ugyanígy, ha a legnagyobb sebességek érdekelnek akkor is az előző módszert kell követnem, azaz addig csökkentem az időlépéseket, míg meg nem kapom a maximumot és az nem változik.
Egyszerű esetekben ezeket elég könnyű belátni és a szimulációk (egyszerű esetekben) valós időben vagy annál gyorsabban oldódnak meg, viszont bonyolultabb esetekben, főleg, ha sokáig tart a szimuláció, nem jó lefuttatni ugyanazt 5-ször és rájönni, hogy még mindig nem elég kicsi az időlépés.
Egyszer réges-régen volt egy szimuláció, ahol egy tengelyt kellett megforgatnom és az össze volt kapcsolva fogaskerék áthajtással több tengellyel. Akkor emlékszem, hogy a megfelelő időlépéssel játszani kellett. Annak a modellnek a komplexitását az jellemezte, hogy amikor kimentettük videóba a mozgást akkor a kis tengely nem forgott. Néztük egy ideig mire leesett, hogy a videó, amit kimentettünk 25 FPS-be volt kimentve, azaz, ha úgy néztük a mozgást, hogy a „nagy” tengely forgott akkor a kis tengely olyan gyorsan forgott, hogy a videóban nem látszott, mert az FPS szám miatt a tengelyhez tartozó fogaskerék fogai kb. egyhelyben álltak. Ezek után jött az, hogy akkor lassítsuk le a mozgást és mentsük ki úgy… ilyenkor meg az volt, hogy a kis tengely forgott, de mivel tök lassú volt a lejátszás, így a nagy tengely szinte állt. Szóval abból a szimulációból nem tudtunk egy darab látványos videót készíteni még úgy sem, hogy a videó kimentésének az FPS számát növeltük.
Előző példánál maradva, hogy mekkora annak a kis tengelynek a vizsgálatához szükséges idő előre becsülhető. Ugyanígy a hozzá tartozó fogaskerék kapcsolat vizsgálatához is becsülhető az idő, igaz a fogaskerék fogainak a találkozását mi abban az esetben a két test mozgásának csatolásával oldottuk meg (egy ilyen csatolás látható ebben a webinárban akkor amikor a két kereket összekapcsolom a 29. percben).
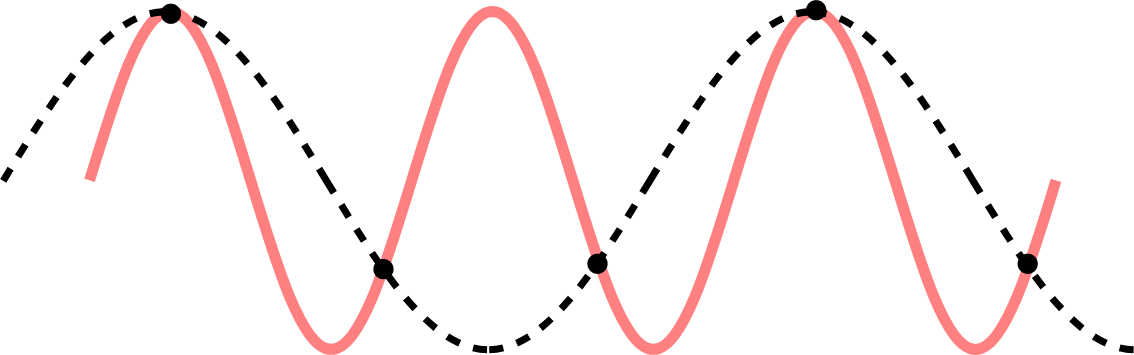
Mi az idő becsléséhez akkor a Nyquist–Shannon mintavételezési tételt vettük alapul. Ezt a módszert én méréstechnikából és rezgésdiagnosztikából hallottam sokat még a főiskolai tanulmányaim során. Ez a mintavételezési tétel azt mondja ki, hogy a mintavételező jelnek legalább kétszer gyakoribbnak kell lennie, mint a vizsgált jelnek. Azaz, ha van egy szinuszosan változó jelem, aminek a frekvenciája 1 Hz (azaz 1 periódus/másodperc), akkor a mintavételezésnek 2 Hz-nek (2 periódus/másodperc, azaz 0,5 másodperc/periódus) kell lennie. Ez azt jelenti, hogy ha van egy szinusz hullámom akkor ahhoz, hogy a mért pontokra ugyanazt a szinuszt tudjam ráilleszteni kell legalább két pont, egy mondjuk a „csúcsra” és egy „gödörbe”. Mivel a megfogalmazásban benne van a legalább szó, így ebből az adódik, hogy ha ennél sűrűbb egyáltalán nem baj. A következő képen az látható, hogy van az eredeti jelem (folytonos vonal) és ritkább a mintavételezés (fekete bogyók) mint az eredeti jel frekvenciája, így a mintavételezési pontokra illesztett szinusz függvény (szaggatott vonal) nagyobb periódusú, mint az eredeti jel.
Visszakanyarodva a kis tengelyre. Ha tudom, hogy annak a forgási sebessége 60 RPM (csak hogy könnyű legyen számolni), azaz 60 fordulat/perc, akkor 1-et fordul másodpercenként. Ha ezt az 1 RPS-t szeretném vizsgálni akkor 0,5 másodpercnél kisebbnek kell lennie az időlépésemnek, azaz a 0,49999 másodperc is már jó, de ha lehet akkor annál azért látványosan legyen kisebb.
Ha megvan a leggyorsabban forgó alkatrészünk, akkor célszerű úgy választani a kezdeti időlépéseket, hogy egy fordulást 3-szor vagy 4-szer lassabban vizsgáljunk. Ezek után az, hogy az időlépésektől független eredmény már az 1/4 forgási sebességű mintavételezési frekvenciánál jelentkezik vagy a forgási sebesség 10-edéig vagy 50-edéig kell lemenni, az a vizsgált mennyiségtől függ. Ha csak gyorsulás és sebesség jellegű eredményeink lesznek, akkor valószínű, hogy a forgási sebesség 1/3-a, 1/4-e elégséges, ha ütközések vagy erőhatások akkor valószínűleg lejjebb kell menni ennél is.
A bejegyzés végében csak annak a kis tengelynek forgási sebességéről írtam, de igazából ezt a tételt célszerű használni a kezdeti időlépés becsléséhez akkor, ha az erők változnak ciklikusan vagy valamilyen random függvény szerint vezéreljük az erőket/elmozdulásokat.
Bízom benne, hogy aki elolvasta ezt a bejegyzést és az előtte lévőket, a közeljövőben magabiztosabban használja a szimulációs szoftvereket. Én jelen pillanatban nem látom, hogy mi lehetne ennek a blogsorozatnak a következő része, így, ha valakinek a sorozat elolvasása után felmerült valamilyen kérdése jelezze 😉 . Jó szimulálást!
Hálózós blogsorozat részei:
- Kellően sűrű a hálóm? I.– Lokális hálósűrítés SE Simulation-ön belül
- Kellően sűrű a hálóm? II. – Most akkor legalább 3 vagy 5 elem kell?
- Kellően sűrű a hálóm? III. – Feszültség gyűjtőpontokkal és hálófüggetlenségi vizsgálat
- Kellően sűrű a hálóm? IV. – Lokális hálósűrítés és konvergencia vizsgálat FLOEFD-n belül
- Kellően sűrű a hálóm? V. – Adaptív hálósűrítés és konvergencia vizsgálat FLOEFD-n belül
- Kellően sűrű a hálóm? VI. – Időlépés meghatározása SE Motion-ben
- Kellően sűrű a hálóm? VII. – Szilárdtest, héj, tartó – elemtípusok Solid Edge Simulation-ben
Források:
[1] Wikipédia: Nyquist–Shannon sampling theorem – File:CPT-sound-nyquist-thereom-1.5percycle.svg https://en.wikipedia.org/wiki/File:CPT-sound-nyquist-thereom-1.5percycle.svg