Ez a blogbejegyzés ötlete a 2021-es FB Live sorozatunk 2021.08.17-ei részével indult, melyet felhasználva elkészült a Kellően sűrű a hálóm? I.  és a Kellően sűrű a hálóm? II.  blogbejegyzés.

Az előző blogbejegyzésben a lokális hálósűrítést mutattam be a Solid Edge Simulation-ön belül. Ebben a bejegyzésben a feszültséggyűjtőpontokról és egy hálófüggetlenségi vizsgálatról fogok írni. Terveim szerint két további Kellően sűrű a hálóm? bejegyzés lesz, ahol a Simcenter FLOEFD-t és a Solid Edge Motion-t hálózását fogom bemutatni.

A blogsorozat előző része és a további részek (ha elkészülnek) a bejegyzés alján található linken érhetőek.

Azok számára, akik arra kíváncsiak, hogy mikor kell abbahagyni a hálósűrítést (és tisztában vannak a feszültségszingularitással) nekik azt javaslom, hogy tekerjenek le a blogbejegyzés aljára a „Visszatérve a feszültségek változására, a sarokban azt láttuk” kezdetű részhez.

 

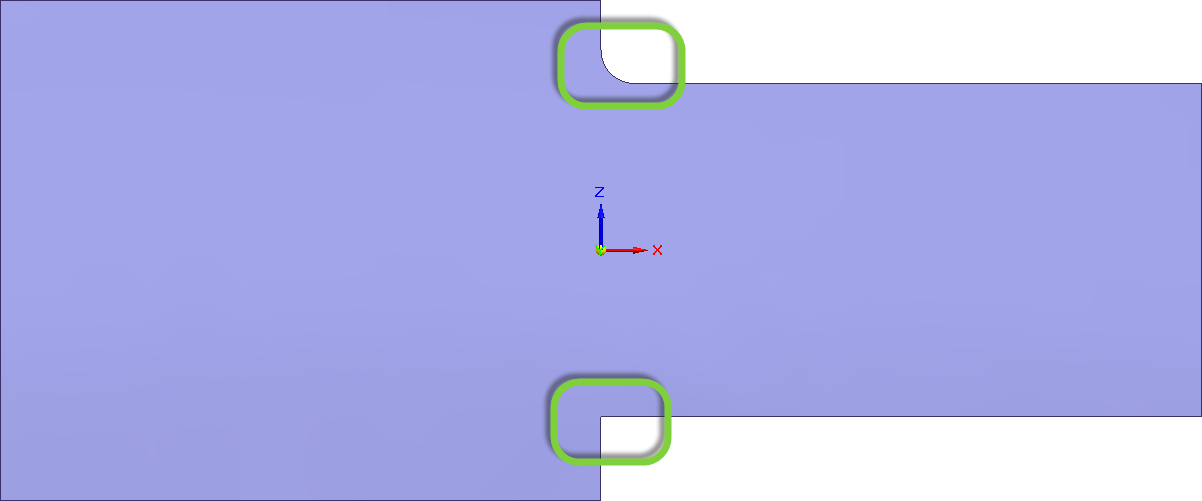
Az előző bejegyzésben azt mutattam be, hogy hogyan lehet végeselemes hálót sűríteni, ebben a bejegyzésben ezt fogom alkalmazni a következő ábrán látható modellel VEM hálójának sűrítéséhez.

 

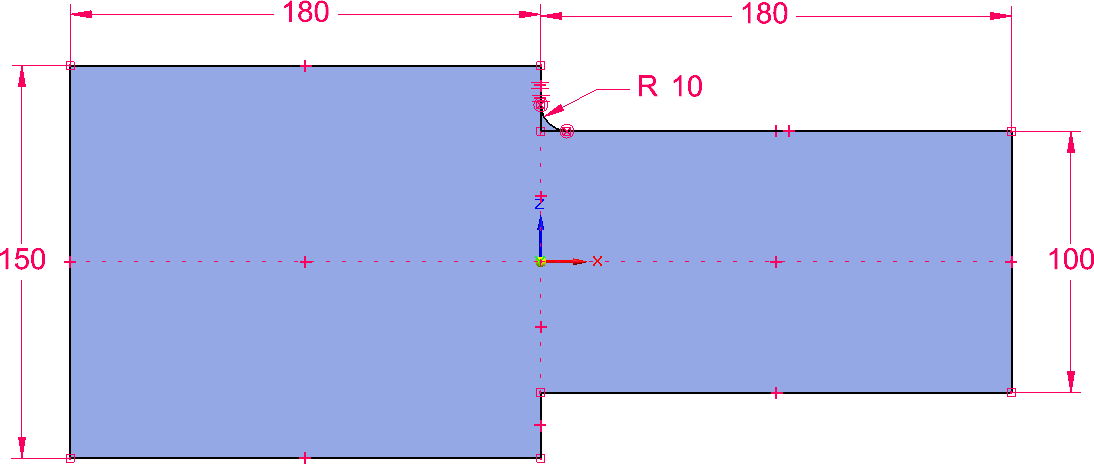
A modell egy felületmodell, amit 2D-s elemekkel hálózok be. A modell méretei a képen láthatók, illetve a geometria „láthatatlan mérete” a vastagsága, melyet 10 mm-re állítottam. A kezdeti háló a következő ábrán látható.

 

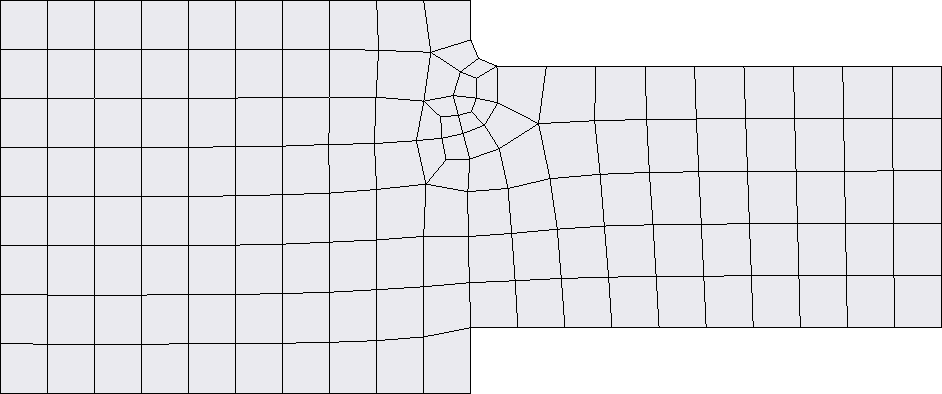
A modell bal oldalát (150 mm-es oldal) rögzítettem, míg a jobb oldalt (100 mm-es oldal) megterheltem 50000 N X irányú erővel. Tiszta húzásként a 180 mm-es hosszokon a σ=N/A képlettel tudom kiszámolni a feszültségeke, mely 50 MPa és 33,333 MPa. Amennyiben ránézek a feszültségeloszlásra a következőt kapom.

 

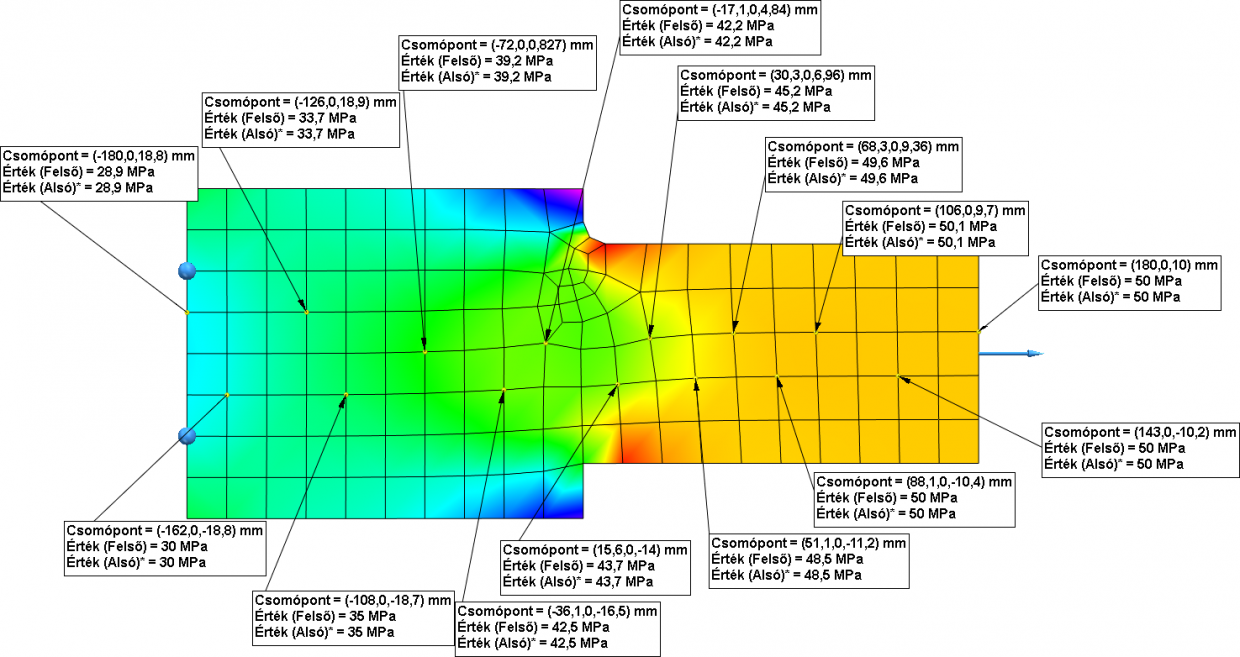
A feszültségeloszláson látom, hogy a lekerekítés és a tökéletes sarok környékén a feszültségek nem egyenletesek. Középen sem az 50, sem a 33,33 MPa nem jött ki mindenhol, melyre a de Saint-Venant elv ad magyarázatot. A következő ábrán ez az elv látható.

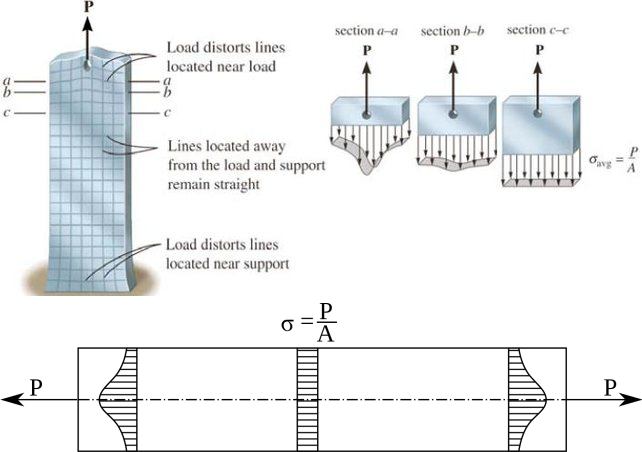
Képek forrása [1] és [2]

 

Az ábra alapján megállapítható, hogy kellő távolságra a terheléstől és a kinematikai kényszerektől (megfogások, rögzítések…), illetve a feszültséggyűjtőpontoktól az átlagfeszültség kialakulhat. Ez így tök jó, valószínűleg, ha sűrítem a hálót akkor lesznek a test közepén olyan pontok, amik hozzák az 50 MPa-t és a 33,333 MPa-t. Ebben az esetben szerintem az az érdekes, hogy a lekerekítésnél és a tökéletes saroknál mi történik, ugyanis az iskolában megtanították, hogy feszültséggyűjtő pontok, azaz onnan fog elindulni a repedés és a törés is. Viszont azt, hogy mekkora ott a feszültség nem sűrűn mondták el… Jó hír, vannak feszültségkoncentrációs táblázatok, illetve akiket a miért érdekel, nekik ott a törésmechanika és a hozzá tartozó fizikai és matematikai háttere [3]. Amennyiben rákeresünk egy esetre és a hozzá tartozó feszültségkoncentrációs táblázatra (pontosabban grafikonra), akkor a következő ábrán látható diagramhoz hasonlót találunk.

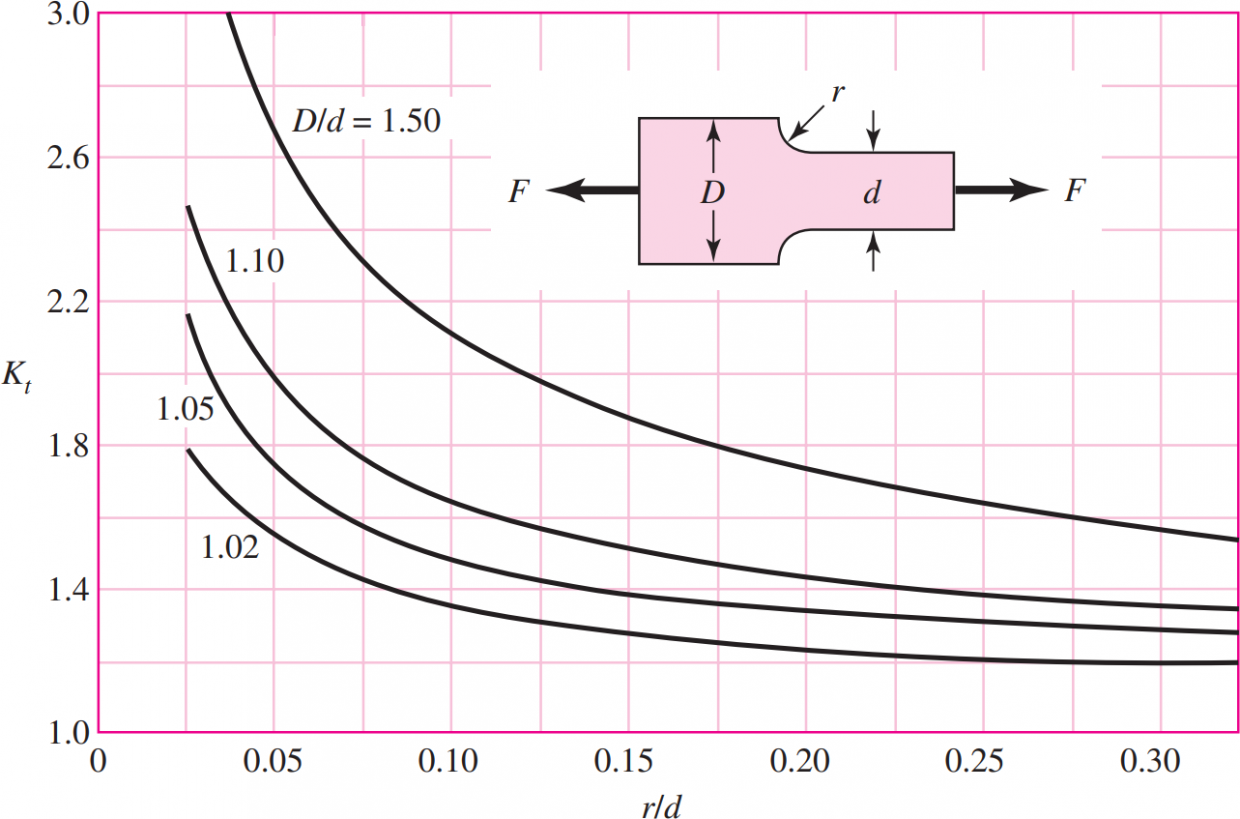
Kép forrása [4]

 

A beillesztett ábra azt mutatja meg, hogy ha van a rajta látható teheresetem (vagy egy ahhoz hasonló) akkor a lekerekítésben mekkora a feszültség. Nézzük nálam a D = 150 mm, a d = 100 mm, azaz a D/d viszony 1,5, így a legfelső folytonos vonal írja le a feszültséghez a kiterjesztési tényezőt. A sugár r = 10 mm, így az r/d arány 0,1. Ha a 0,1-es r/d aránynál elindulok felfelé a D/d vonalat kb. Kt = 2,1 – 2,15-nél metszi. Ezek után elő kell venni az átlagfeszültségre vonatkozó képletet, azaz a σ=N/A-t (vagy a de Saint-Venant ábrákon a σ=P/A-t). Ha képlet alapján 50 MPa-t várok a d-hez tartozó szakaszba, ezt az 50-et meg kell szoroznom a kiterjesztési tényezővel, azaz a Kt-vel. Ha Kt = 2,1 akkor 105 MPa, ha Kt = 2,15, akkor 107,5 MPa a várt feszültség a lekerekítéshez.

Ha az előző 105-107,5 MPa-t le szeretném ellenőrizni VEM-en belül, akkor a hálózásomat sűrítenem kell az előző blogbejegyzésben látott módszerek egyeikével, majd a kiértékelésnél a kialakuló feszültségeket kell vizsgálnom. A legnagyobb feszültség a Színskála fülön a Max jelölés paranccsal kényelmes követni, míg a lekerekített és a tökéletes sarokkal ellátott éleken a Vizsgálat parancs Él menti lekérdezése szerintem a kézenfekvő megoldás.

 

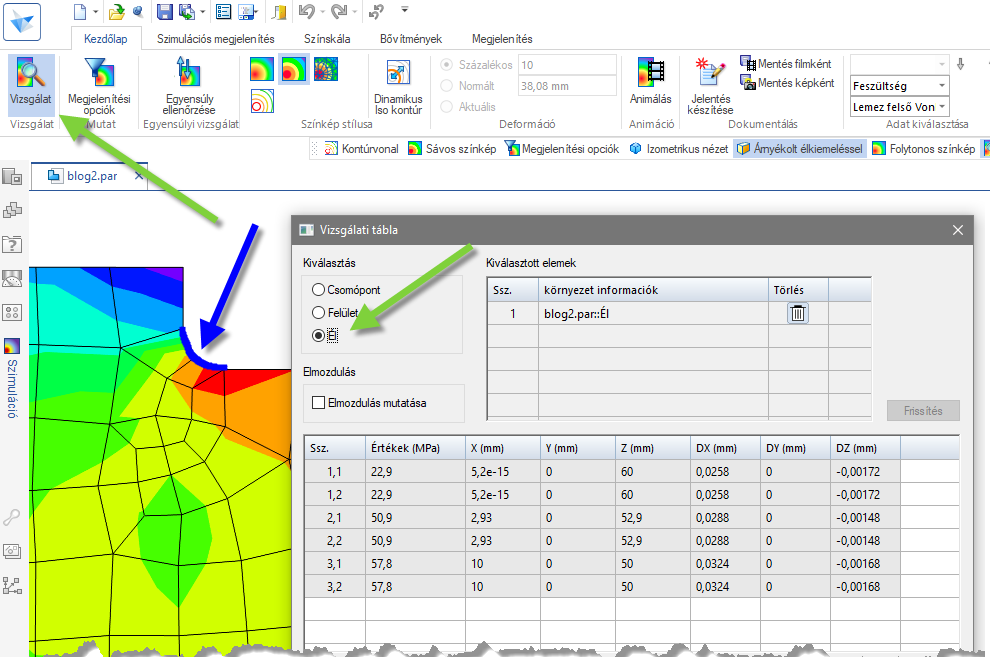
Az első három esetben csak a globális hálót sűrítettem, melyek a következő ábrán láthatók.

 

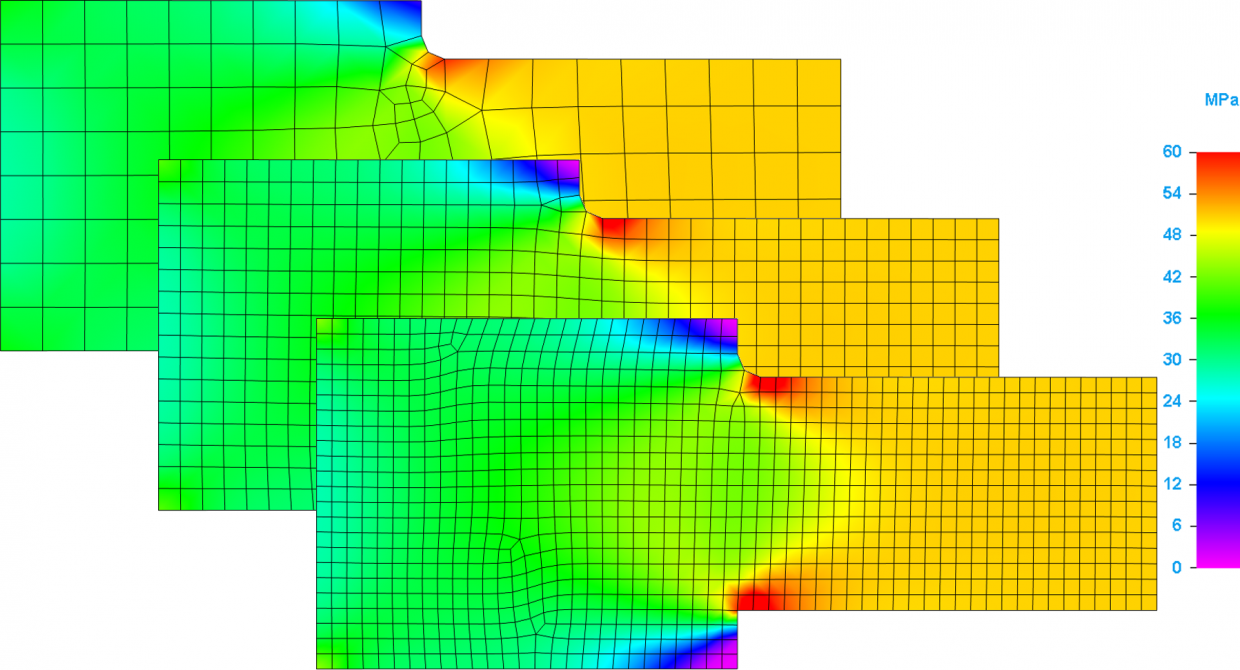
Az ezt követő esetekben mind a globális mind a lokális hálót sűrítettem. A lokális hálósűrítések a lekerekített felület és a tökéletes sarokpont környékén találhatók. A negyedik állapot, egy köztes és az utolsó állapot látható a következő képen.

 

Minden egyes esetben amikor sűrítettem a hálót leírtam a vizsgált pontokon a feszültséget és a csomópontjainak számát, mely a következő ábrán látható.

 

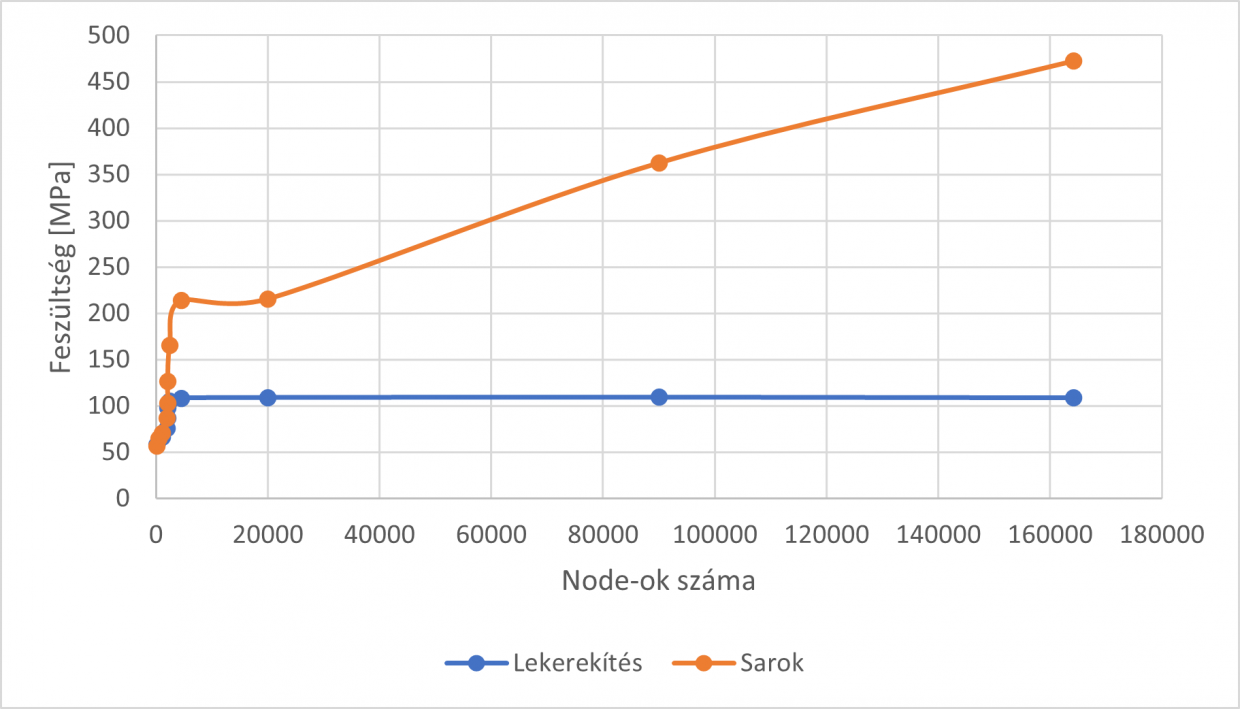
Az ábrán megfigyelhető, hogy a lekerekítéshez tartozó feszültség alakulása (kék vonal) egy kezdeti értékről indul, majd el kezd nőni és pár lépés múlva beáll egy közel vízszintesre, azaz a feszültség szemmel nem is látható mértékben változik csak. Ha a sarokpontot nézem (narancssárga vonal), ahol tökéletes sarok van, azaz a két él találkozása 90°-os szöget zár be, ott a feszültség a lekerekítéshez hasonlóan nőni kezd, majd növekszik tovább. A sarok esetén a 4509 és a 20049 között a feszültség csak 2 MPa-val nőt, ennél a lépésnél valószínűleg nem sűrítettem elégé a hálót.

 

Nézzük akkor van a lekerekített élhez tartozó feszültséggyűjtőpont, ami valós feszültséget tartalmaz és ha kellően sűrű hálóval futtatom a szimulációt akkor megbízható eredményt ad. Ide vártam azt a kiterjesztési tényezővel növelt feszültséget (105-107,5 MPa), ami a legutolsó esetben 108,5165 MPa lett. A kettő közötti különbséget még a szimuláció előtt jóval nagyobbra tippeltem volna, mert a Kt kiterjesztési tényező leolvasásánál van egy leolvasási hiba.

Van az alsó pont, ahol a feszültség megy a végtelen felé, itt feszültség szingularitás alakul ki, mely a végeselemes módszer matematikai háttere miatt alakul ki. FONTOS, ez a hiba a végeselemes módszer hibája, nem a Solid Edge Simulation hibája, hanem a VEM-é, azaz minden másik szoftverben (pl. Femap vagy Simcenter 3D) is megtalálható.

A jelenségre a gyors válasz az, hogy azért alakul ki, mert deriválni csak folytonos függvényt lehet és a sarokpontban két nem folytonos geometriát leíró függvény fut be, azaz egy vízszintes és egy függőleges. Ha deriválni szeretném a vízszintes geometriát leíró függvényt és a függőlegest, akkor az OK, de a sarokpontban ezt nem tudom megtenni, mivel ott a geometriai függvény szakad, illetve, ha azt figyelmen kívül hagyom, akkor a sarokban két értékem van, egy a függőlegeshez, egy a vízszinteshez.

Kicsit lassabb válasz a jelenségre az, hogy a feszültségszingularitás oka az, hogy a VEM alapegyenletének (K.u=f, ahol K, a merevségi mátrix, u, az elmozdulásvektor és f, a terhelésvektor) megoldása során az elmozdulás az ismeretlen tag. Miután a megoldó kiszámította az elmozdulást, abból deriválással meghatározza a fajlagos alakváltozást, majd egy szorzással a feszültségeket.

 

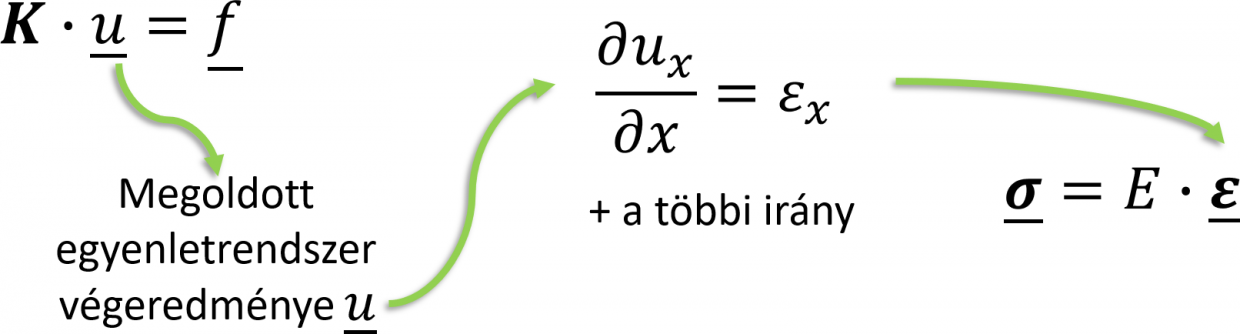
Az előző ábrán látható egyenletekben, K, merevségi mátrix, u, elmozdulás vektor,  f, terhelésvektor, ux, elmozdulás vektor x irányú komponense, ε, fajlagos alakváltozás mátrix, εx, x irányú fajlagos alakváltozás, σ, feszültség mátrix, E, rugalmassági modulus.

Visszatérve a feszültségek változására, a sarokban azt láttuk az előző diagramon, hogy volt egy csomó érték az elején, melyeket egy közel vízszintes görbe követett, illetve volt a sarokpont, ahol szintén az elején rengeteg pont volt, majd utána jött egy növekvő függvény. Ha ezeket nem az elemszám szerint, hanem a vizsgált hálók száma szerint ábrázolom (azaz 1. kiindulási ábra, 2. az első sűrítés, 3. a második sűrítés…) akkor a következő ábrán láthatók szerint változott a feszültség.

 

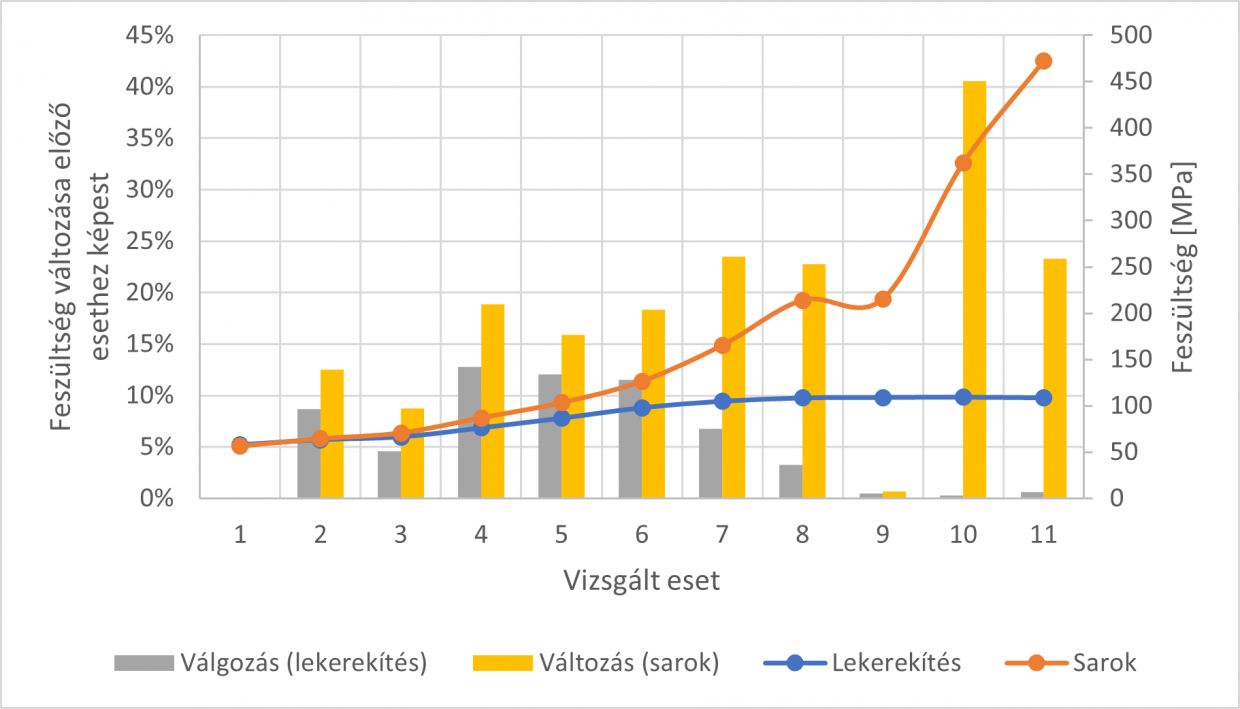
Az előző ábrán a görbék mellett látható egy oszlopdiagram is, melyek az előző hálóhoz képesti változást mutatják (százalékos formában). Ennek a változásnak a nyomonkövetése az egyik módszer arra, hogy mikor kell abbahagyni a hálósűrítést. Nincs kőbe vésve, hogy pontosan mikor kellene abbahagyni a sűrítést, van olyan, aki 5% alá, van olyan, aki 1% alá teszi azt a limitet, ahol abba kellene hagyni a hálósűrítést. Ez az érték iparágtól és tapasztalattól függ.

Az biztos, hogy célszerű legalább három-öt esetet lefuttatni, továbbá, ha lehetőségünk van rá, akkor mindig felezzük az elemméretet. Én azt vettem észre, hogy plusz egy hálósűrítés sohasem árt, mert vannak olyan esetek, (mint most a 9. eset,) amikor pont úgy jött ki a globális/lokális hálósűrítés elemmérete, hogy az előző esethez képest nem tartalmazott nagyon nagy változást. Valószínűleg az előző megállapításra vezethető vissza az is, hogy a feszültségszinguláris pontok nem minden esetben szigorúan monoton növekvő értékek (azaz az értékük nem mindig nő), vannak olyan esetek amikor csökkennek, de a következő sűrítés után megint nőnek.

Ez csupán egy módszer, van olyan, aki arra esküszik, hogy a csomóponti feszültségeket kell összehasonlítani az elemenkénti feszültségekkel és azoknak a különbségét kell levinni pár százalék alá. Sajnos ez a módszer jelenleg nem olyan egyszerűen érhető el Solid Edge Simulation-ön belül, mint Femap-en vagy Simcenter 3D-n belül. Elemenkénti lekérdezés esetén a feszültségeket meghatározása úgy történik, hogy az elemhez tartozó összes csomópontot átlagolja a posztprocesszor, míg csomóponti esetén a „középen” lévő csomópont értéke úgy jön ki, hogy a közvetlenül mellette lévő csomópontok eredményeit is beleátlagolja a posztprocesszor. Tehát, ha van egy négyszög elemem (2D) a sarokpontjain egy-egy node ponttal, akkor az elemenkénti átlagolás ezt a négy értéket átlagolja, míg a csomóponti esetén a központi node-dal összekötött node-okét is, azaz a területi átlag 9 csomópont értékét tartalmazza.

Ezt a fajta kiértékelést jelenleg csak plotolni (ábrázolni) tudjuk a Solid Edge-en belül, viszont lekérdezni nem. Azok számára, akiknek ez fontos lenne készítettem egy fejlesztési javaslatot Ability to Probe stresses on elements címen. Kérem őket, hogy egy „like”-kal támogassák az ötletet. Azok, akiknek egyéb fejlesztési javaslatai lennének, ők a Hogyan tudom a saját céljaim szerint formálni a Siemens termékek jövőjét? korábbi blogbejegyzés alapján tudják ezt beküldeni, vagy rajtunk keresztül a felhasználók elől elrejtett oldalra.

 

Gyors összefoglaló az eddigiekről

Nézzük az előző közel 10 000 karakter összefoglalása ként, ebben a blogbejegyzésben az volt, hogy

• Vannak olyan pontok/helyek ahol, ha sűrítem a feszültséget, akkor azok a végtelen felé tartanak, ezek a feszültségszingularitások.
• Vannak olyan helyek ahol, ha sűrítem a hálózást kellő sűrűség esetén valós feszültségeket kapok.
• Vannak olyan módszerek, amivel meg tudom állapítani azt, hogy kell-e még sűríteni a hálómat (pl. a feszültségek változásának követése).

 

További gondolatok

További két kérdés merül fel ezek után,

• Mi van akkor, ha mindenhova rakok egy letörést vagy lekerekítést, ami a gyártásnál úgy is oda kerül (ha máshonnan nem, akkor a megmunkálószerszámról egy minimális)?
• Mi van akkor, ha nem rakok sehova sem sarokkezelést?

Az első kérdésre a válasz egyszerű, megtehetjük, viszont akkor azt is be kell hálóznunk, ami idő. Minél kisebb az elemméretem, annál több elemem van, így annál tovább számol a gép, viszont ez egy jó megoldás főleg, ha van erre a célra egy kijelölt gép, vagy ha rendelkezésünkre áll mondjuk egy hétvége, hogy lefusson.

A második számolási idő szempontjából kedvezőbb, viszont ebben az esetben a blogbejegyzés elején használt feszültségkoncentrációs (Kt) tényezőt kell használni. Ez a szimuláció is jó és használható, a benne lévő értékek elfogadhatók és megbízhatók, leszámítva a szinguláris pontokat.

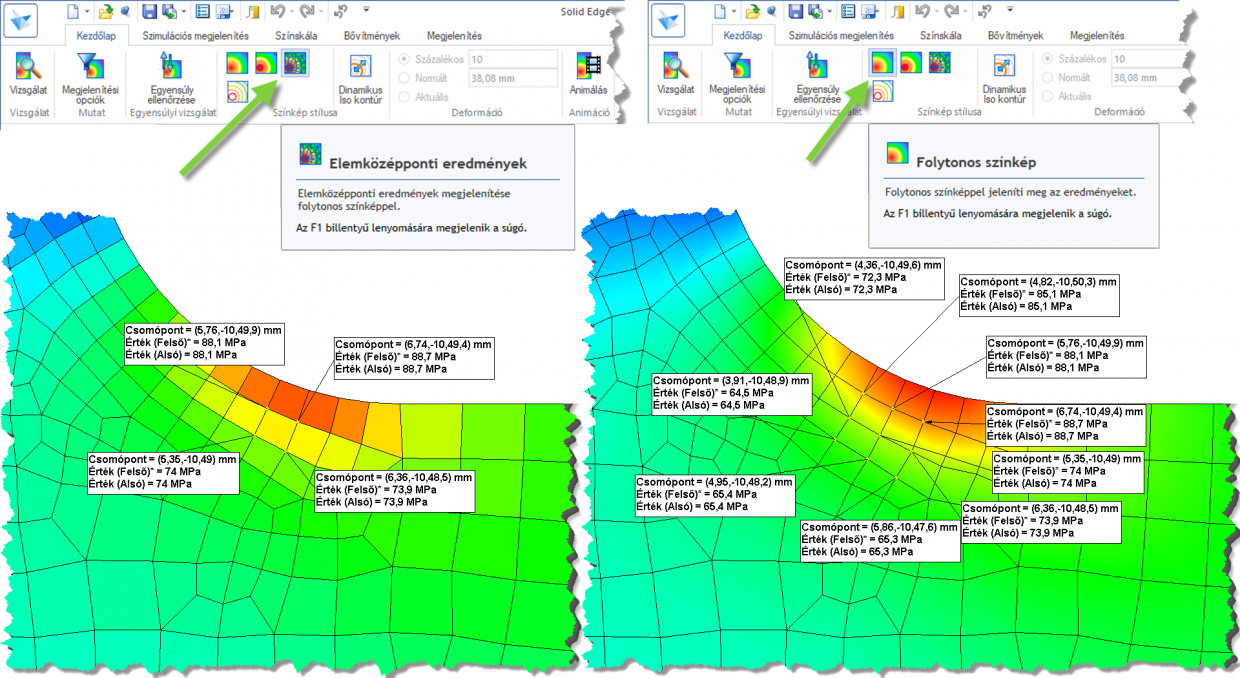
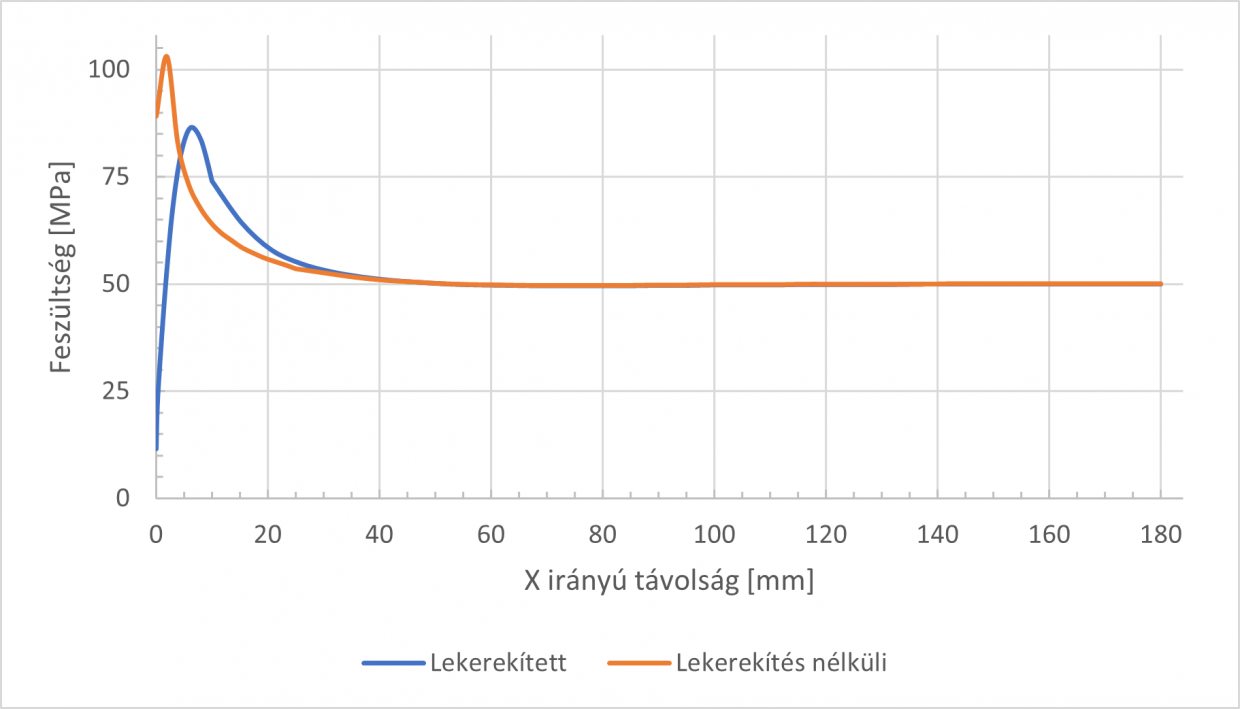
A következő ábrán a lekerekített oldal és a lekerekítés nélküli oldal feszültségei láthatók a test élén.

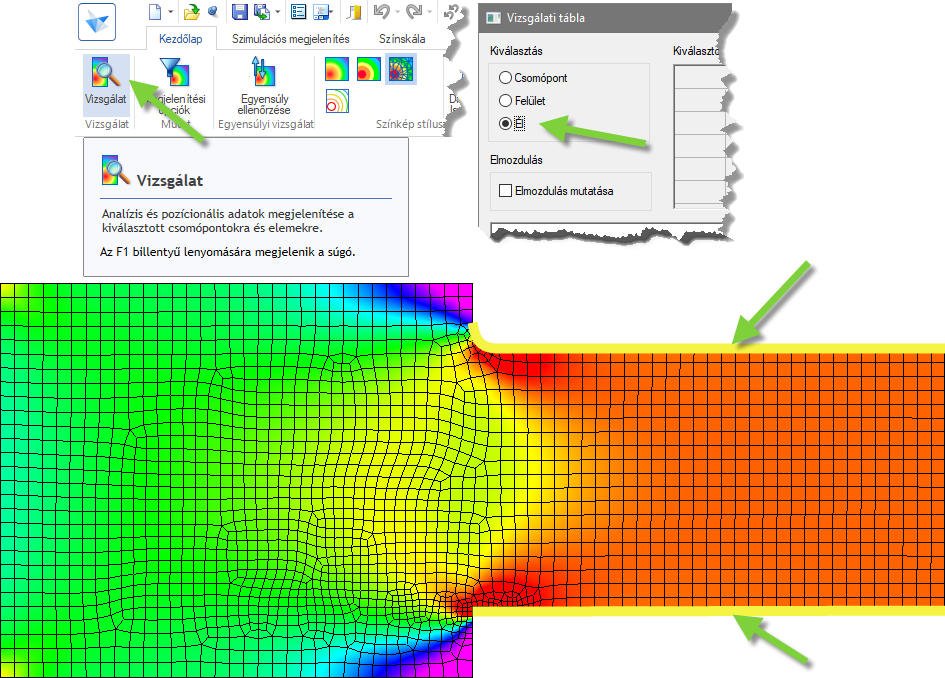
Ehhez a lekérdezéshez a sárgával kiemelt élekre a Vizsgálat/Él parancsot használtam.

A reprodukálhatóság miatt fontos, hogy ennél a lekérdezésnél 5 mm-es átlagos elemméretet használtam, a lekerekítés X irányban 10 mm-nél ért véget, így az a csomópont, amiben a lekerekítéshez tartozó érték már nem szerepel 20 mm-nél (4 db elem) található. A két feszültségérték különbsége 20 mm-nél (4 elem távolság) 2,8 MPa, míg 30 mm-nél (6 elem távolság) 0,4 MPa, illetve 40 mm-nél (8 elem távolság) 0,1 MPa alá csökkent a különbségük. Amennyiben ennél sűrűbb hálóval hasonlítottam volna össze a két élen ébredő feszültséget, azonos elemszámú távolságra, hasonló különbségeket kaptam volna.

Nézzük akkor a következő kérdést, hogy akkor most mi legyen, kell a lekerekítés vagy nem kell?

Erre egyértelmű választ nem tudok adni, vagy olyan ökölszabályt, hogy ha R = 10 mm akkor kell, amúgy meg nem, vagy ha a teljes hossz 1%-ánál kisebb a lekerekítési sugár akkor nem kell. Sajnos ilyen szabályok nem léteznek (vagy én nem tudok róla), így a kérdésre a válasz szerintem az, hogy ha fontos a lekerekítés, azaz a lekerekítésben vizsgálom a feszültséget akkor kell, még akkor is, ha sokkal sűrűbb háló kell oda és sokáig fut így a szimuláció. Amennyiben nem fontos a lekerekítés, és csak a keresztmetszetben vizsgálom a feszültségeket és a sarokkezelések nem befolyásolják a deformációt és a feszültségeket nagyon, akkor nem.

Csak sarokban léphet fel feszültség szingularitás?

Sajnos nem, vannak egyéb pontok, ahol számíthatunk szingulartiásra, ilyen a pontszerű terhelések és rögzítések helyei, illetve a kontaktok esetén a pontszerűen érintkező helyek.

A bemutatott modellben volt másik szinguláris pont?

Nem tudom, mert máshol nem vizsgáltam, viszont valószínűleg a rögzített él két szélső pontja is az volt.

Záró kérdés: Van más hibája is a szimulációknak (úgy általánosan)?

Igen, ilyen például a számábrázolási hiba, azaz a megoldók nem végtelenül pontosan számol a szoftver, hanem csak „néhány” tizedesjegy pontossággal. Itt ehhez bele kellene menni a numerikus számábrázolásba és abba, hogy milyen a 8 bit-es számábrázolás vagy a 16 bit-es, de az nagyon tudományos lenne, egyszerűbb, ha úgy állunk neki, hogy adjuk össze háromszor az 1/3-adot. Ha végtelenül sok tizedesjegyem van, akkor 1/3 + 1/3 + 1/3 = 1, viszont, ha mondjuk két tizedesjegy pontossággal vizsgálom ezt, akkor 0,33 + 0,33 + 0,33 = 0,99, ami nem 1.

Ami a számábrázolási hibánál is gyakoribb, az a hálózási hiba, azaz a diszkretizációs hiba, mely rejtve benne volt ebben a blogban és az előzőben is. Ez a hibaforrás belátható gondolati síkon is, ha van egy furatom, ami a CAD-en belül tökéletes kör, azt, ha behálózom akkor a háló élei egyenesek, azaz a körből poligon lesz a hálózás után. Minél jobban besűrítem a hálót, annál kisebb lesz az eltérés a kör és a poligon között. Tökéletes kör sűrítés során (lineáris elemekkel) sohasem lesz, viszont van az a kis elemméret, ahonnan a két eredmény azonosnak tekinthető (ehhez kell egy hálófüggetlenségi vizsgálat).

További hibák és hibaforrások is vannak, például, ha beírt erő a valóságban nem ugyanannyi, vagy ha nem azzal az anyaggal szimulálok, mint ami a valóságban van (pl. eltér pár százalékot a rugalmassági modulus), viszont ezeket felsorolni és mindenre felkészülni előre lehetetlen.

 

Bízom benne, hogy van olyan, aki elolvasta ezt a blogot és nem zavartam össze teljesen és nem vettem el a kedvét a szimulációktól. Záró gondolatként George Box-ot tudom idézni „All models are wrong but some are useful”, azaz minden modell rossz, de akad köztük néhány hasznos, azaz tudjuk, hogy sarokban nem tudunk deriválni, így a végeselemes módszer nem mindenhol használható, de amúgy a többi helyen jó. Jobbat vagy nem ismerünk, vagy nem alkalmazható olyan könnyen általános célokra, mint a VEM.

 

Hálózós blogsorozat részei:

• Kellően sűrű a hálóm? I.– Lokális hálósűrítés SE Simulation-ön belül
• Kellően sűrű a hálóm? II. – Most akkor 3 vagy 5 elem kell?
• Kellően sűrű a hálóm? III. – Feszültség gyűjtőpontokkal és hálófüggetlenségi vizsgálat
• Kellően sűrű a hálóm? IV. – Lokális hálósűrítés és konvergencia vizsgálat FLOEFD-n belül
• Kellően sűrű a hálóm? V. – Adaptív hálósűrítés és konvergencia vizsgálat FLOEFD-n belül
• Kellően sűrű a hálóm? VI. – Időlépés meghatározása SE Motion-ben
• Kellően sűrű a hálóm? VII. – Szilárdtest, héj, tartó – elemtípusok Solid Edge Simulation-ben

Felhasznált források

[1] De Saint-Venant elv https://es.wikipedia.org/wiki/Principio_de_Saint-Venant
[2] Sheelan Hama: Theory of Elasticity – Lecture 2: Two Dimensional Problems in Cartesian Coordinate System, https://www.researchgate.net/publication/329611654_Two_Dimensional_Problems_in_Cartesian_Coordinate_System
[3] Knowledge dbase on
Design of Machine Elements -Stress concentration factors  https://www.ux.uis.no/~hirpa/6KdB/ME/stressconc.pdf
[4] Budynas and Nisbett: Shigley’s Mechanical Engineering Design, 8. kiadás, pp. 1026- 1034, http://research.iaun.ac.ir/pd/jjfesharaki/pdfs/UploadFile_9038.pdf
[5] George Box idézet: https://en.wikipedia.org/wiki/All_models_are_wrong