Ennek a blogbejegyzés sorozatnak az első három részében a Solid Edge végeselemes moduljával, azaz Solid Edge Simulation-nel és annak a hálózójával foglalkoztam. Ebben és a negyedik a bejegyzésben a Simcenter FLOEFD-vel, azaz a numerikus áramlástani (CFD, Computational Fluid Dynamics) modullal foglalkozom, mely elérhető Solid Edge-en és NX-en belül is. Az NX-es és a Solid Edge-es modul között tudásban és kezelőfelületben nincs különbség (leszámítva az SE és az NX CAD rendszerből származó dolgokat, melyek CAD specifikusak, pl. Solid Edge esetén ilyen a QuickPick). Az előző blogban a FLOEFD hálózóját és annak lokális hálósűrítéseit mutattam be. Jelen bejegyzésben az adaptív hálósűrítést és egy hálófüggetlenségi vizsgálatot ismertetek.

Az előző bejegyzésben bemutatott eszközök tök jók, ezekkel kellene sűríteni a hálót és eljátszani azt a hálófüggetlenségi vizsgálatot, amit az harmadik részben írtam. Azok számára, akik nem biztosak abba, hogy milyennek kellene lennie a jó hálónak, nekik segítség, az adaptív hálózás. Az adaptív hálózás egy automatikus hálózó, ami ott sűríti a VT (végestérfogat) hálót, ahol az áramlástani jellemzők változnak. Ezt több esetben lehet használni, például:

• hálófüggetlenségi vizsgálatnál,
• akkor, ha még nem tudjuk (vagy csak sejtjük), hogy milyen hálóra lenne szükségünk,
• olyan esetekben amikor a szimuláció első iterációjától az utolsóig nem lenne gazdaságos mindenhol nagyon sűrű hálóval szimulálni.

Az első eset szerintem nem szorul kifejtésre, a második eset az, amikor egy új terméket vizsgálok és még nem szimuláltam sohasem olyat. Példának legyen egy számomra teljesen új eset az előző blogbejegyzésben lévő szárnyprofil. Ha én ezt az esetet először futtatom és nem hallottam róla még, hogy a belépő oldalon van egy torlópont, ahol az áramlási térben hálósűrítésre van szükségem. Ugyanígy a profil végén a kilépő élnél is kell sűríteni a hálót az áramlási térben és az utána kialakuló csóvarégióban is. Ez a két sűrítés mellett a szárnyprofil felületén célszerű határréteg hálót létrehozni. Ezt követően, ha nem a mostani esetet nézem, azaz az áramlási sebesség nem X irányú, hanem azzal valamilyen szöget zár be, hanem mondjuk 5-10° vagy annál nagyobb, akkor számítanom kell arra, hogy a repüléstechnikából ismert átesés jelenségére, ilyenkor a szárnyprofil környezetét is sűrítenem kell, illetve megfontolandó, hogy a most bemutatott állandósult állapot helyett időfüggő szimulációt futtassak.

A harmadik esetben, azaz amikor nem lenne célszerű minden iterációt nagyon sűrű hálóval lefuttatni, arra példának azt tudom felhozni, hogy van egy kétfázisú áramlásom (víz és levegő, víz és olaj stb.) úgy, hogy kezdeti állapotban csak az egyik közeg van jelen. A szimuláció során ebbe az áramlási térbe „befolyatok” egy adott térfogatú közeget a másik fázisból és annak az útját vizsgálom. Ebben az esetben, ha még azt sem tudom, hogy merre folyna a másik fázis, előre felesleges lenne mindenhol besűríteni az áramlási teret. Majd, ha elfolyt teljes egészében az egyik térrészről, akkor ott célszerű lenne ritkítani a hálót, mert feleslegesen sűrű. Ebben az esetben az automatikus hálósűrítést és ritkítást az adaptív hálózó meg tudja tenni nekünk és mindig csak annyi elemem lesz a szimulációban, amennyit beállítok.

Az adaptív hálózásról készítettem egy tudásbázis bejegyzést, mely a következő videón érhető el:

További tudásbázis videók érhetőek el a support oldalunkon. Illetve videók eléréséről egy áttekintő olvasható korábbi blogunkban.

Ha az adaptív hálósűrítést használva a 15-ször sűrítettem a hálót. Első képen a kiindulás háló látható, majd a jobb láthatóság miatt elrejtettem az elemhatárokat jelző fekete vonalakat és utána a 15 sűrítésből néhány kép kiemelve látható.

Megfigyelhető ezeken az ábrákon, hogy a hálósűrítés az utolsó három eseteben szemmel alig látható. Ez azért van, mert a hálózó olyan helyekre is rakott egy-egy kicsi (piros) cellát, ami elveszik a narancssárga és sárga elemek között. Ha számszerűsítem az elemek számát, akkor (az első esetben, azaz) a kiindulási hálónál 18 581 elemem volt összesen, amiből 137 cella csonkolt volt, míg az utolsó esetben, (ahol a kiindulási cellához képest 5-ször sűríthetett a hálózó) 428 075 elemem volt, melyből 69 952 elem volt a szilárdtest és a folyadéktérfogat határán.

Az előzetesen ismertetett szimulációnál állandósult állapotot vizsgáltam, azaz, ha lefuttatom a szimulációkat, akkor utána van egyetlen egy eredményem. Ezeket az eredményeket, ha beírom egy táblázatkezelőbe, akkor az eredmények hálófüggőségét ugyanúgy tudom követni, mint az előző bejegyzésben a végeselemnél.

Abban az esetben, ha futás közben bekapcsolom a Goal Plotot, akkor a szimuláció során nyomon követett mennyiségeket (Goal-okat) a szimuláció futása közben is nézni tudom. Ez azért van így, mivel a CFD-s megoldók klasszikusan iteratív megoldók, így minden iteráció után az értékük lekérdezhető.

Ez a funkció a következő képen látható és az Insert Goals Plot (Ctrl+G) paranccsal kapcsolható be.

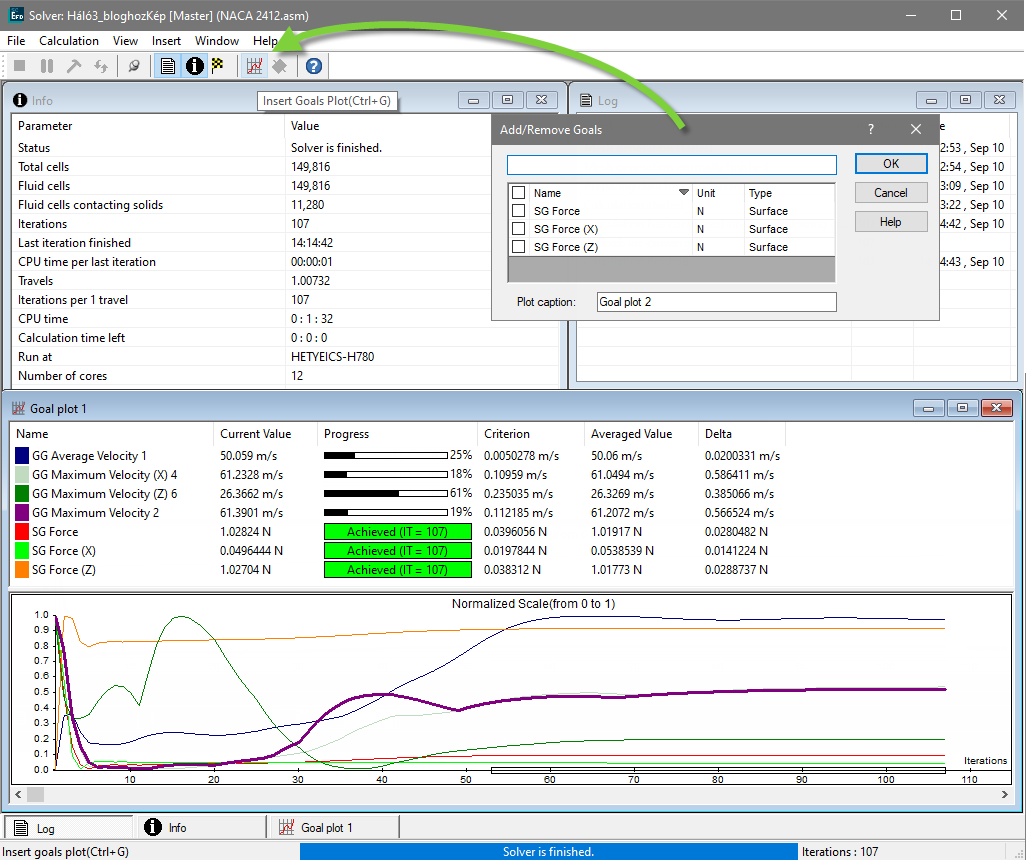
A Gola Plot az előző képen alul látható. Itt az ablakon belül vannak a kilistázott megfigyelt mennyiségek. Itt az látható, hogy az SG Force és a többi erő a 107. iterációnál konvertált be, míg a sebességek 18-61%-ig konvergáltak be az adott iterációnál. (Ezt a képet a 107. iterációnál mentettem le, ha tovább futtatom a szimulációt akkor ezek az értékek is jobban be tudtak volna konvergálni.) Ebben az alsó ablakban még azt is látom, hogy mennyi az adott iterációnál a vizsgált mennyiség értéke, illetve a kritériumérték, ami alatt konvergensnek tekinti a FLOEFD megoldója az értéket, illetve itt megtalálható az összes iteráció átlaga és még egy különbség érték is.

Ezek az értékek alatt látható, hogy iterációról iterációra, hogyan változott a vizsgált paraméter. Jelen esetben egy normalizált érték látható a függőleges tengelyen, a vízszintesen az iterációk.

Amennyiben állandósult állapotú szimulációt futtatok, akkor alapbeállítás szerint az addig fut, míg a nyomon követett mennyiségeim, azaz a Goal-ok be nem konvergálnak, vagy egy virtuális mennyiség a Travel 4 nem lesz. (A travel egy virtuális részecske, ami az áramlási tér két legtávolabbi pontja között vándorol, ha az értéke 1, az azt jelenti, hogy egyszer tette meg ezt az utat, ha 4, akkor négyszer tette meg az utat a két legtávolabbi pont között.) Amennyiben a Goal-ok bekonvertáltak vagy elérte a szimuláció a 4 travelt, akkor a szimuláció leáll. Ha nem az alapbeállításokat használom és még be is kapcsolom az adaptív hálózást akkor ugyanez az ablak a következő képen néz ki.

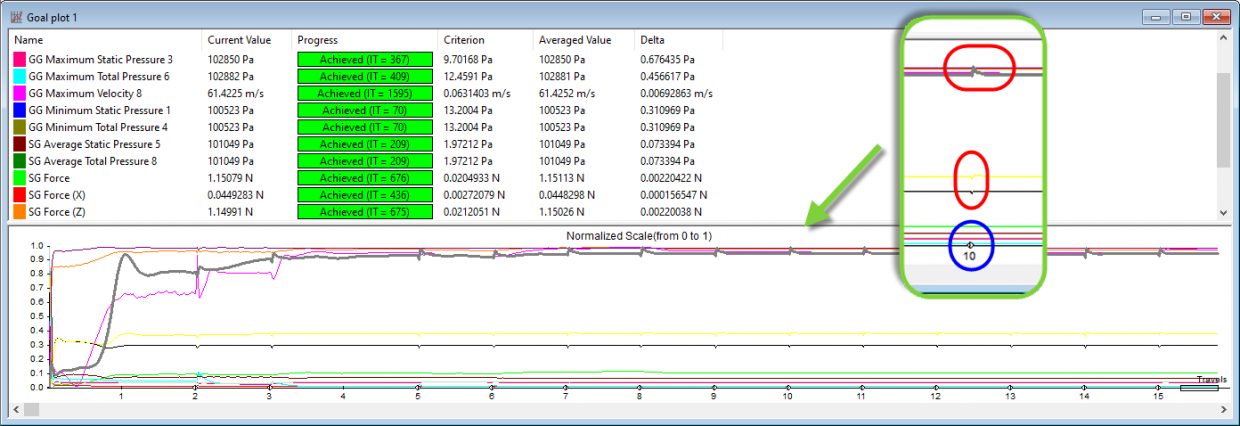
Az előző ábrán az látható, hogy megváltoztak az előző Gola Plot-hoz képest az aktuális értékek és a hozzájuk tartozó kritérium, átlag és delta értékek. Ezek közül a konvergencia kritérium, amit kiemelnék, ez azért változik, mert sűrűbb lett a háló, és alapbeállítás szerint ennek az értéke automatikusan változik.

A numerikus adatokon kívül a diagram is megváltozott, egyrész a vízszintes tengelyen nem az iterációk vannak, hanem a Travelek száma, másrészt néhány helyen ugrások láthatók a megfigyelt mennyiségekben. Az ugrások az adaptív hálózás miatt vannak, amiket úgy állítottam be, hogy minden egész travelnél legyen. Az újrahálózást a Goal Plot egy hegyére állított négyszöggel jelöli, melyet kékkel kiemeltem a nagyított ábrán. Az ugrások, ugyanígy a nagyított ábrán pirossal vannak kiemelve. Az ábrán továbbá az is megfigyelhető, hogy az újrahálózás okozta hiba, pár iterációval később eltűnik, és a megfigyelt mennyiségek konvergálnak egy fix érték felé. Amennyiben két hálósűrítés között nem változik a megfigyelt mennyiség értéke, az azt jelenti, hogy az eredményem hálófüggetlen.

A megoldás közben látható Goal Plot utólag is elővarázsolható a Post-processzálás során, melyhez a Results kategórián belül a Goal Plots menüben létre kell hoznunk egy lekérdezést. Az így létrehozott Plot megjeleníthető a FLOEFD-n belül (Show) és kiexportálható xlsx-be (Export to Excel) is.

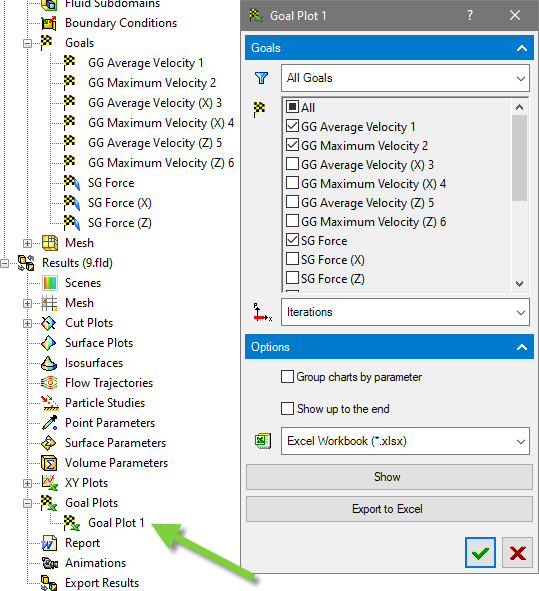
Én, ha FLOEFD-n belül hálófüggetlenségi vizsgálatot futtatok, akkor az előző blog és a mostani módszereit vegyesen használom, azaz először pár szimulációt lefuttatok és ott az eredmények alapján sűrítem a hálót ott, ahol szükségesnek érzem. Ha megvan, így a kiindulási hálóm és még úgy érzem, hogy további sűrítések szükségesek, vagy ha időfüggő szimulációt futtatok, akkor a turbulencia vagy a szabadfelszín jobb felbontása miatt az adaptív hálózóval még pár lépésben rásűrítek az eredményekre.

Hálózós blogsorozat részei:

• Kellően sűrű a hálóm? I.– Lokális hálósűrítés SE Simulation-ön belül
• Kellően sűrű a hálóm? II. – Most akkor legalább 3 vagy 5 elem kell?
• Kellően sűrű a hálóm? III. – Feszültség gyűjtőpontokkal és hálófüggetlenségi vizsgálat
• Kellően sűrű a hálóm? IV. – Lokális hálósűrítés és konvergencia vizsgálat FLOEFD-n belül
• Kellően sűrű a hálóm? V. – Adaptív hálósűrítés és konvergencia vizsgálat FLOEFD-n belül
• Kellően sűrű a hálóm? VI. – Időlépés meghatározása SE Motion-ben
• Kellően sűrű a hálóm? VII. – Szilárdtest, héj, tartó – elemtípusok Solid Edge Simulation-ben