Ez a blogbejegyzés (terveim szerint) egy öt részes bejegyzésnek a második része.

Az előző bejegyzésben azt mutattam be, hogy hogyan lehet Solid Edge Simulation-ön belül sűríteni a végeselemes hálót. Az előző blogbejegyzésben segítségemre volt a 2021-es FB Live sorozatunk 2021.08.17-ei része, azaz a „Kellően sűrű a VEM hálóm? Lokális hálósűrítés Solid Edge Simulation-ön belül”. A Facebook videóban a felvezető diáknál volt egy pár kép arról, hogy az eredmények hogyan térnek el a hálózás függvényében (3 perc 40 másodpercnél). Ebben a blogbejegyzésben az a két dia látható kicsit kifejtve.

A későbbiekben ezt a bejegyzést (terveim szerint) még egy végeselemes, egy áramlástani és egy dinamikai, bejegyzés követi, melyeknek a linkjei majd ennek a blogcikknek az alján (lesznek) találhatók.

Az említett két dián, egy hálófüggetlenségi vizsgálat látható egy befalazott tartóval. Ebben az esetben még nem fogok eljutni arra a pontra, hogy mennyi elemet kellett volna használni, hanem csak addig, hogy ökölszabály szerűen, kb. hány elemre lesz szükségem. A dián a következő ábrán a tartó és annak a Solid Edge Simulation-ös modellje látható (K keresztmetszet 20 mm-re található a tartó végétől).

 

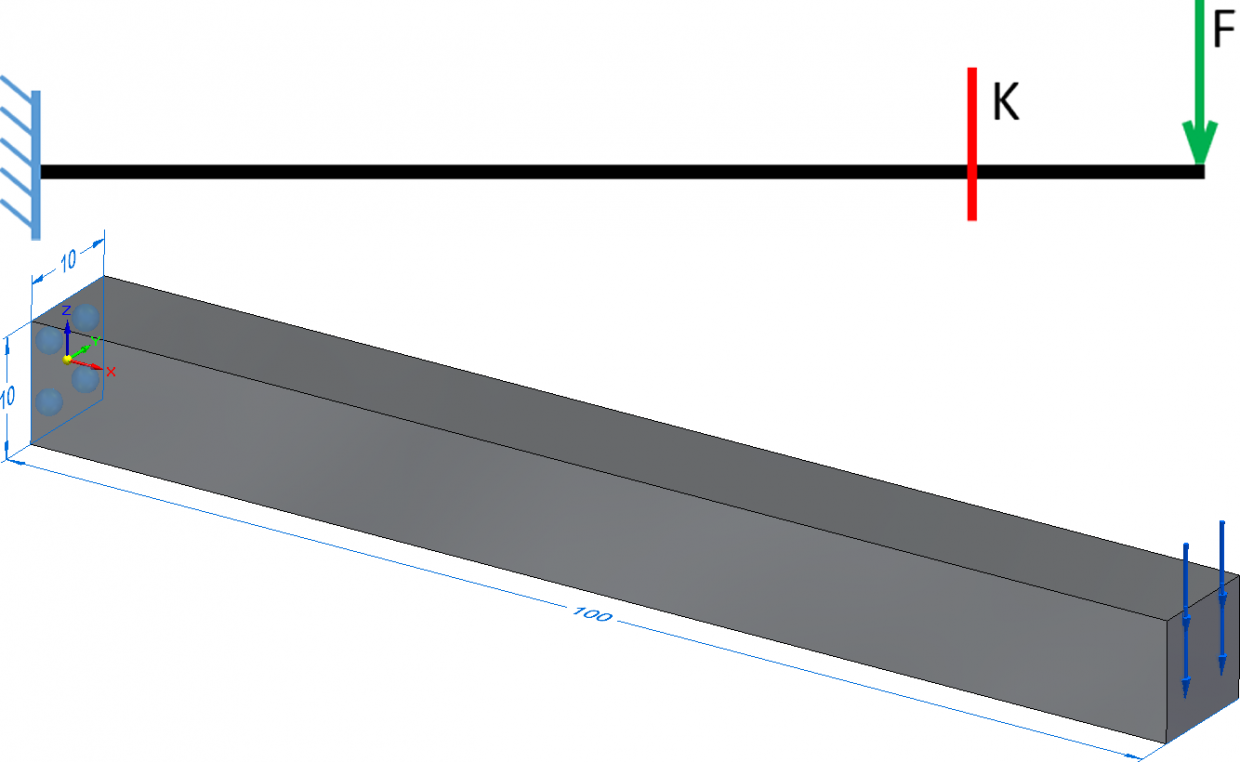
A Live prezentációjában ez a 10×10 mm-es keresztmetszetű szilárdtest látható, ahol készítek egy olyan végeselemes hálót, ahol az átlagos elemméret 10 mm, azaz a keresztmetszet mentén egy elemem van. Ennek a szimulációnak a hálója és a vele lefuttatott szimuláció látható a következő ábrán.

Az ábra felső képén csak a végeselemes háló látható, a középső képén a szimuláció eredménye és az alsó képen a szimuláció eredménye a végeselemes háló nélkül. A terhelő erő, amit alkalmaztam 100 N. A terhelés nagyságához képest az alakváltozások elég nagynak tűnnek, ennek az oka annyi, hogy a Solid Edge Simulation felnagyítja az eredményeket, hogy jobban lássam (az elmozdulás 0,198 mm volt a valóságban, a képeken a teljes modell befoglaló méretének a 10%-ára van felnagyítva, azaz 10,1 mm-re).

 

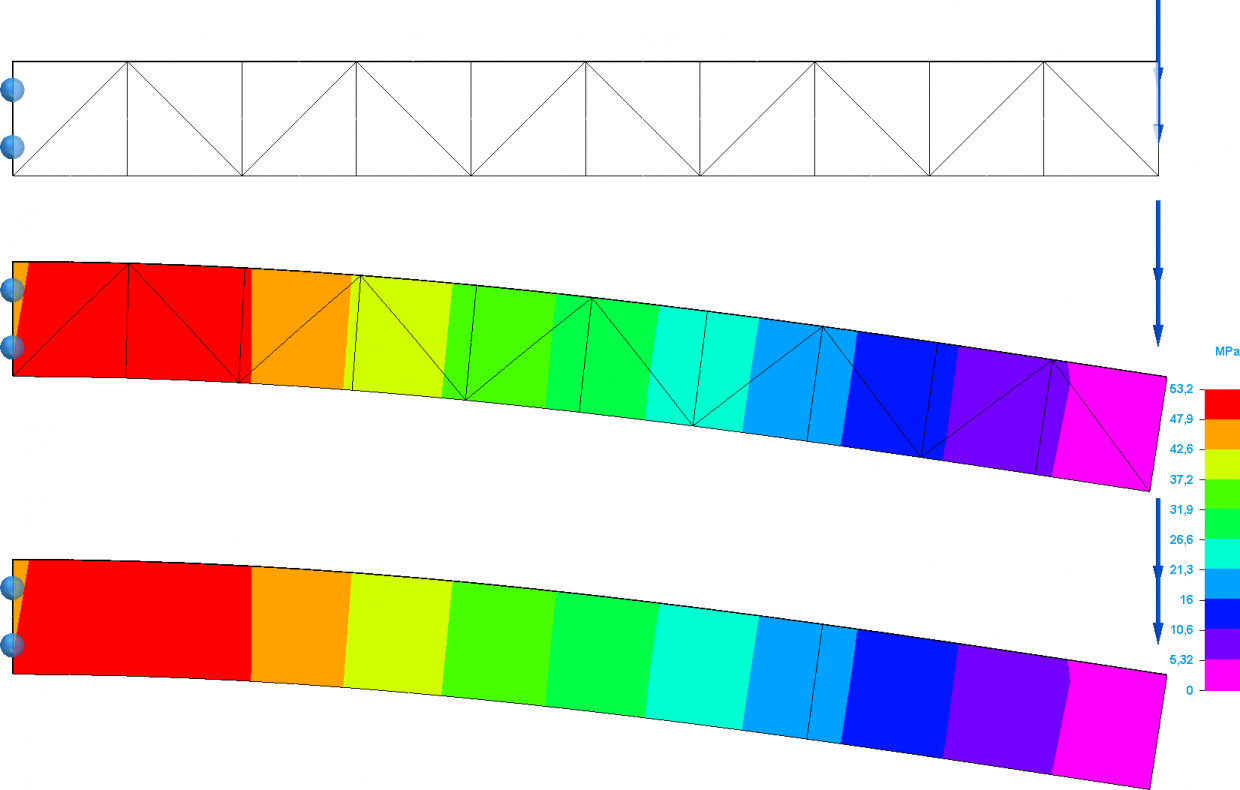
Mielőtt továbbmennék a hálósűrítéssel előtte nézzük meg az eredményeket. Felül kellene látnom egy húzott szálat, alul egy nyomott szálat és középen egy semleges szálat. Ez itt hiányzik, mert a vastagság mentén egy elemem van. Számolási csomópont (azaz node), alapértelmezett esetben csak az elemek csúcspontjánál található, tehát ha megnézem a mechanikai modellemet, látom, hogy a K keresztmetszetnél csak a húzott és a nyomot szálat számolta ki.

 

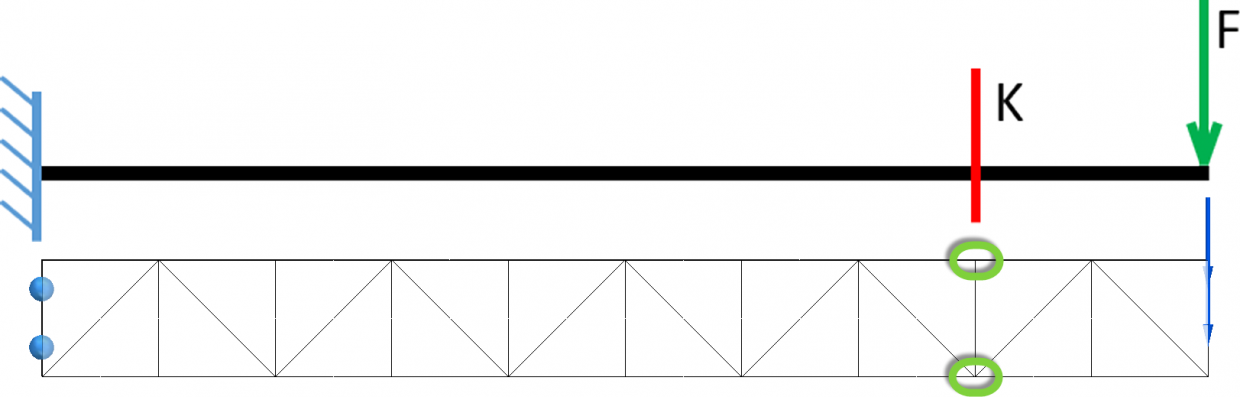
Ha nagyon szeretném ezen a ponton át tudok menni a plotok között a Von Mises feszültségről a normálirányú feszültségre és ott az X irányú komponensnél rá tudom fogni, hogy ott a húzott, nyomott és a semleges szál, de valójában csak „fent” kiszámolta a szoftver a feszültség értékeket, majd „lent” is (ezek amúgy +18 és -18 MPa lett) és ezeket utána összekötötte és így kijött középre a semleges szál…

 

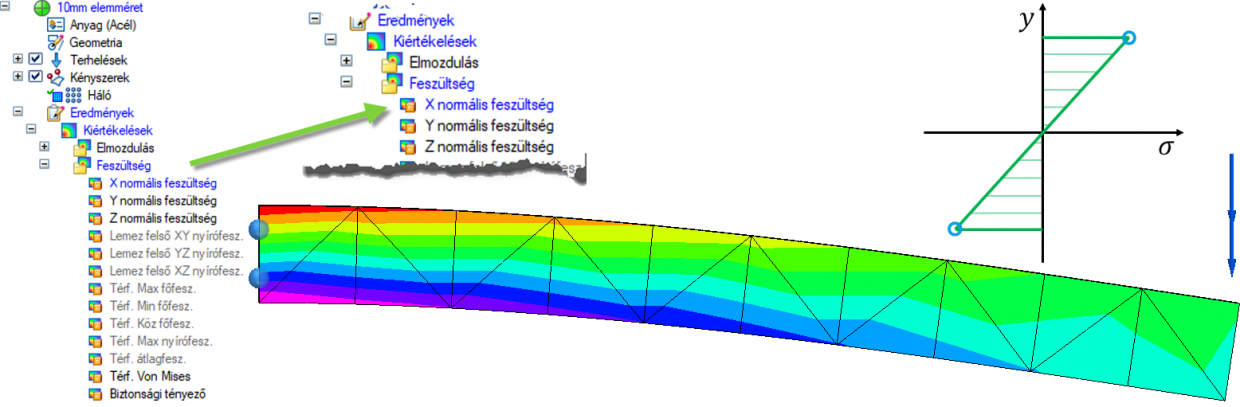
Az előző ábrán látható, hogy a semleges szálat „kihozta a matek”, viszont sokkal jobb lenne, ha nem kijönne csak, hanem ténylegesen ki is számolná a szoftver. Így miután lefuttattam ezt a szimulációt 10 mm-es elemmérettel, ennek a felére, azaz 5 mm-re állítottam az átlagos elemméretet, mely 2 elemet jelent a vastagság mentén.

Ebben az esetben a von Mises féle egyenértékű feszültség a következő ábrán láthatóan alakult. Az ábrán megfigyelhető, hogy fent is piros, lent is piros, középen meg magenta, azaz a feszültségkomponensek is kiadják azt, hogy középen van egy semleges szál (az egyenértékű feszültség képlete alapján nincs negatív érték, így fent is és lent is „pirosat” kaptam, azaz pozitív számot).

 

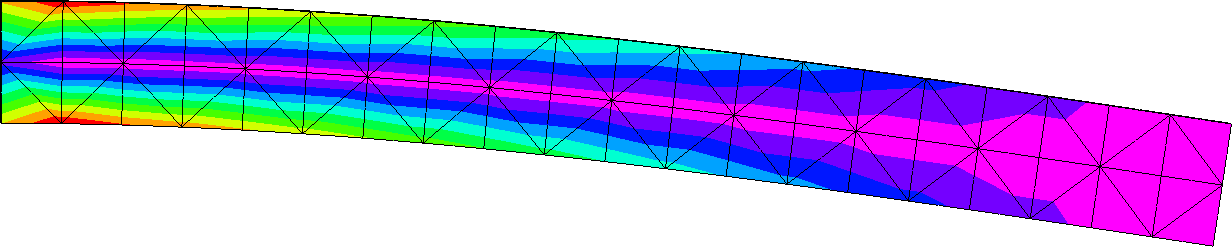
Ha megnézem az X irányú normál feszültséget, akkor azt látom, hogy ott két számolási pont volt a keresztmetszet mentén, és feszültségkomponens két „oldala” eltérő előjelű, illetve azt, hogy így a középső 0 MPa, azaz a semleges szál is számolt érték.

 

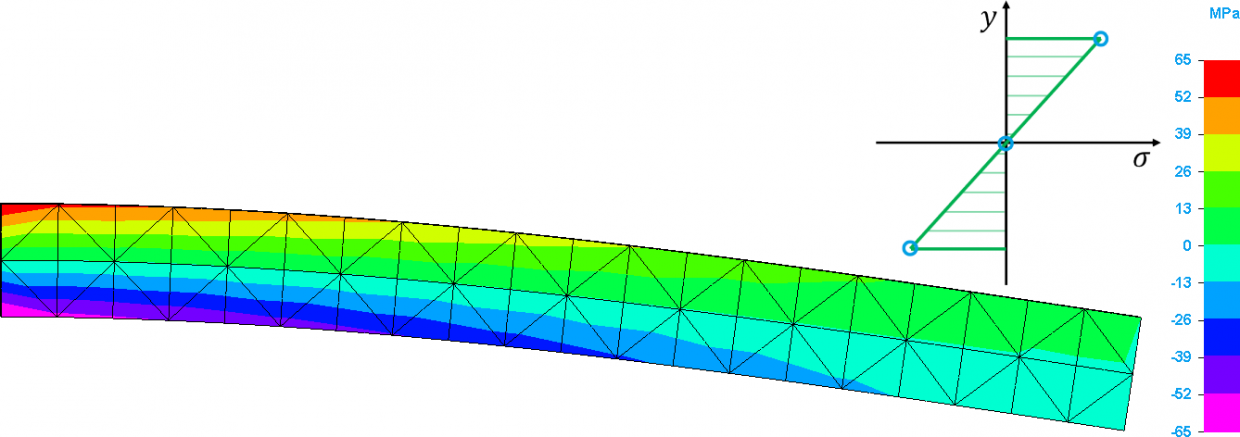
Ha tovább sűrítem a hálózást 2 mm-es elemméretre, akkor öt elemmel számol a keresztmetszet mentén a Nastran kód a Solid Edge Simulation-ön belül és az előzőhöz hasonló eloszlást kapok.

 

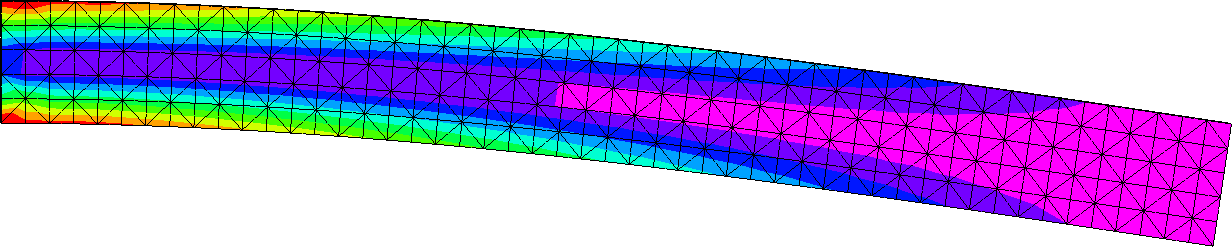
És az előzőhöz hasonló a feszültségeloszlást az X irányú normálfeszültség esetén.

 

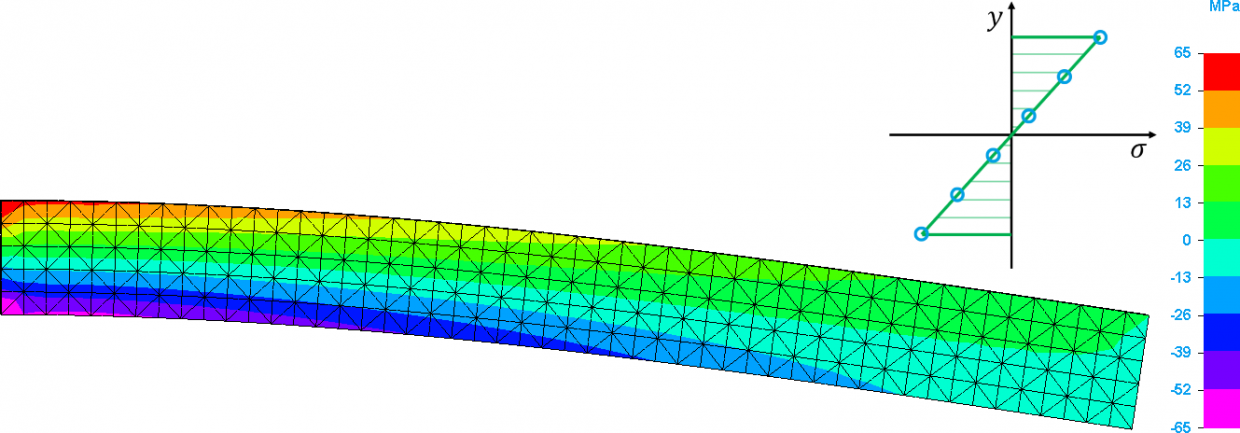
Ezek után, ha sűrítem a hálót 1 mm-re, akkor 10 elemmel számol a szoftver a teljes keresztmetszet esetén, és a következő von Mises féle egyenértékű feszültséget kapom.

 

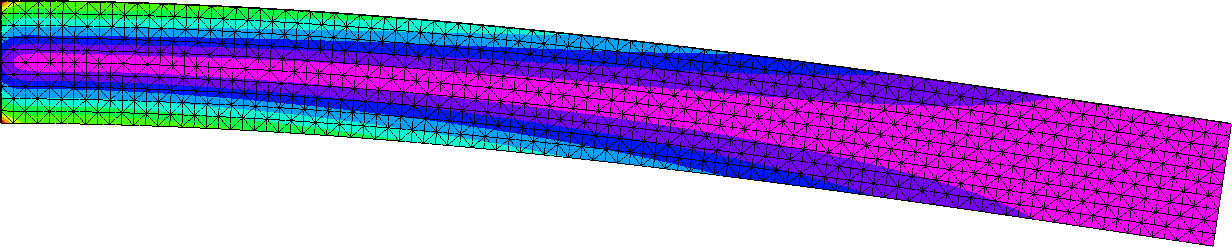
És az előzőkhöz hasonló a feszültségeloszlást az X irányú normálfeszültség esetén.

 

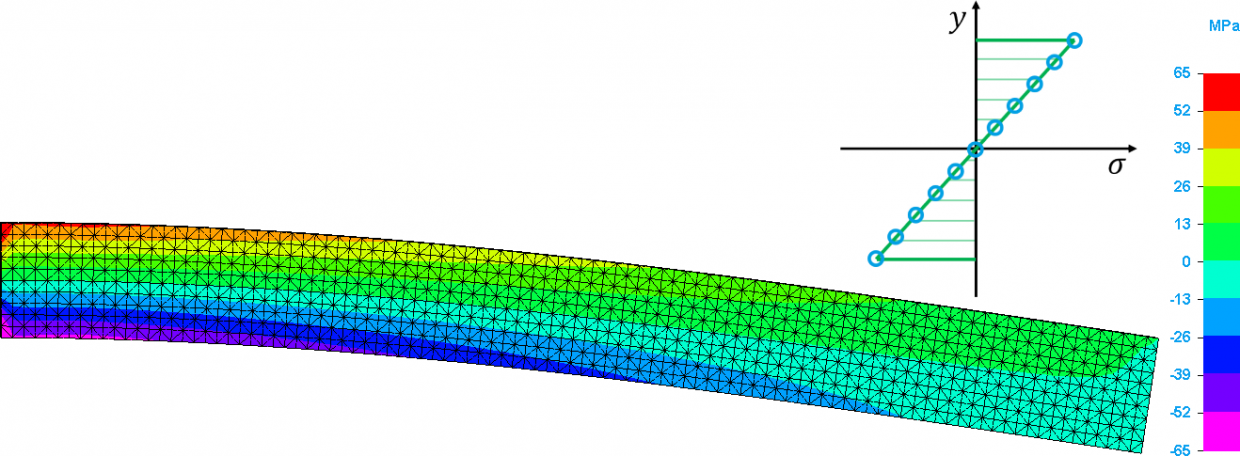
Ezt követően a hálózást még egyszer sűrítettem 0,5 mm-es elemméretre, ahol a feszültségeloszlások az előzőkhöz hasonlóan alakultak. Amennyiben a K keresztmetszet feszültségeit egy diagramon ábrázolom, akkor az a következők szerint alakul.

Nézzük erre az esetre mikor kellett volna abbahagyni a hálósűrítést? Ha megnézem a feszültség értékeket akkor látom, hogy 0,15 MPa-n belül volt a legsűrűbb és a legritkább hálóesetek közötti feszültség különbség (von Mises feszültség a húzott szálban). Ha a következő diagramot nézem, akkor az utolsó lépésnél az ötödiknél, ahol az átlagos elemméretem 0,5 mm volt (ezt az esetet nem fényképeztem ki, mert kinézetre úgy néz ki, mint az 1 mm-es eset).

 

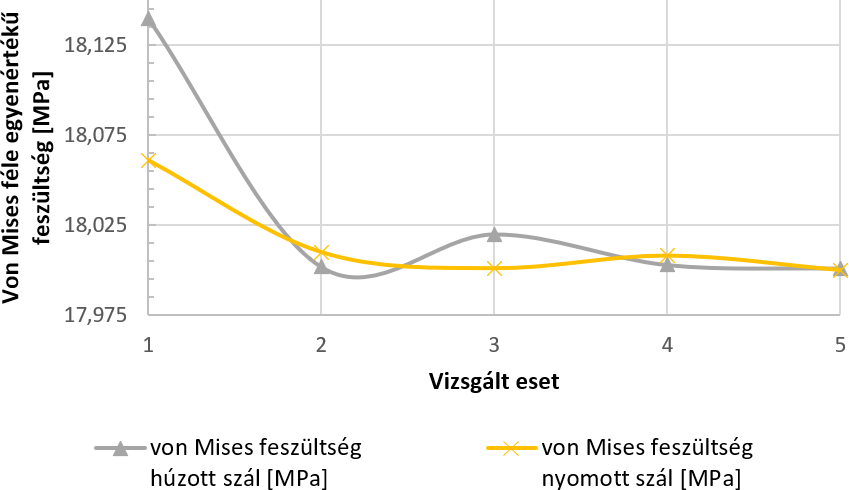
Az előző ábrán azt látom, hogy a feszültségek eltérése 0,15 MPa-on belül volt a legritkább és a legsűrűbb esetekben. Az, hogy ez mit jelent és hogyan kellene kiértékelni arra a következő bejegyzésben adok egy-két tanácsot.

Ha nem a feszültségértékeket nézem, hanem a feszültségeloszlást a hálózás függvényében, akkor azt látom, hogy ahol 3 számolási pontom volt, az a háló kezdő hálónak jónak tűnik, mivel itt megvolt a húzott, a nyomott és a semleges szál is. Ha ehhez a 3 csomóponthoz még egyet hozzáadok (biztonsági tényező), akkor 4 csomópontom lesz, ami 3 db elemet jelen. Az előző biztonságitényezős elemszám gondolatmenetére hivatkozva szokták azt mondani, hogy 3 db elem a minimális elemszám, amit a falvastagság mentén használni kell. Akik nagyobb biztonsággal szeretnének elemszámot javasolni, mivel nem minden esetben tiszta hajlítás lép fel, ők az 5-öt elemet szokták minimálisan javasolni.

Ha nem a fenti hajlítás példáját nézzük, akkor a nyírással is le lehet vezetni a hálóhoz szükséges minimális elemszámot, hiszen két elemnek (vagy node-nak) el kell mozdulnia ellenkező irányba ahhoz, hogy a középen lévő harmadik elem (vagy node) nyíródni tudjon. Utóbbi nyírt példához, ha „hozzáadjuk” a biztonsági tényezőt és belevesszük azt, hogy a prím és a páratlan számok gyakran előjönnek az ökölszabályoknál, akkor belátható, hogy megint a 3-5 elemnél vagyunk, mint minimális elemszám.

Ez az elemszám tiszta hajlításnál és tiszta nyírásnál könnyen belátható, viszont bonyolultabb eseteknél, ahol a feszültségek eloszlása nem lineáris ott nem jó.

 

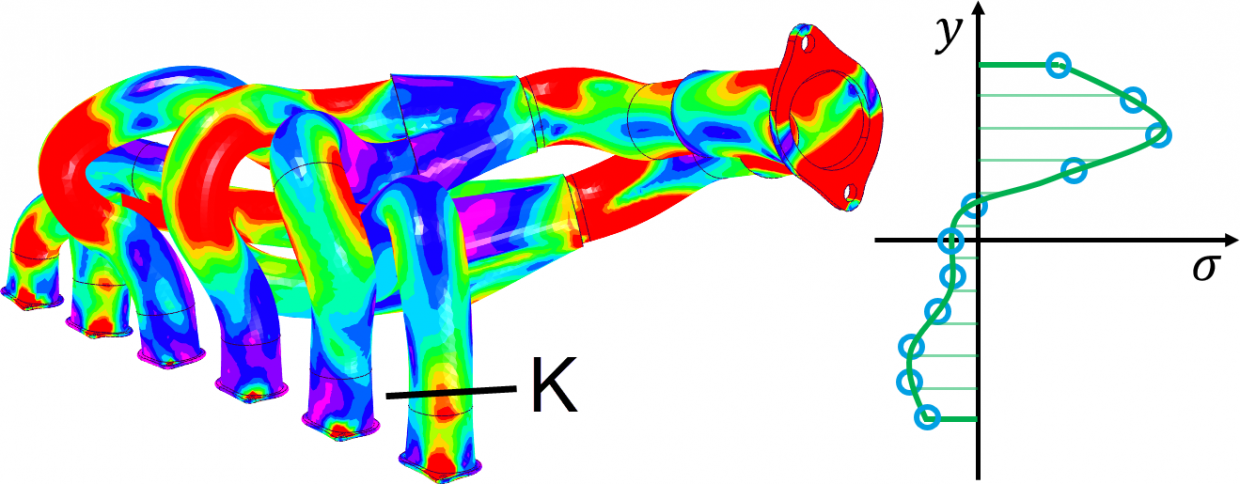
Tételezzük fel, hogy a K keresztmetszet az ábrán tömör és ott a feszültségeloszlás nagyon nem lineáris és az ábra melletti függvény szerint változik. Ebben az esetben a 3-5 db elem/keresztmetszet ökölszabály nem működik. Itt elő kell venni egy táblázatkezelő programot és az elemsűrítések után a vizsgált pontokat össze kell hasonlítani (ez az összehasonlítás lesz a következő bejegyzésnek a témája).

 

Hálózós blogsorozat részei:

• Kellően sűrű a hálóm? I.– Lokális hálósűrítés SE Simulation-ön belül
• Kellően sűrű a hálóm? II. – Most akkor legalább 3 vagy 5 elem kell?
• Kellően sűrű a hálóm? III. – Feszültség gyűjtőpontokkal és hálófüggetlenségi vizsgálat
• Kellően sűrű a hálóm? IV. – Lokális hálósűrítés és konvergencia vizsgálat FLOEFD-n belül
• Kellően sűrű a hálóm? V. – Adaptív hálósűrítés és konvergencia vizsgálat FLOEFD-n belül
• Kellően sűrű a hálóm? VI. – Időlépés meghatározása SE Motion-ben
• Kellően sűrű a hálóm? VII. – Szilárdtest, héj, tartó – elemtípusok Solid Edge Simulation-ben