Végeselemes szimulációk során előkerül az a kérdés, hogy mit és hogyan kellene szimulálni ahhoz, hogy ne tartson sokáig, erre egy megoldás szokott lenni, a szimuláció egyszerűsítése. Egyik egyszerűsítési módszer az, hogy ha van egy szimmetrikus szerkezetem szimmetrikus erőrendszerrel, akkor azt félbevágom és egy szimmetriakényszert használok. Míg egy másik módszer, hogy elemtípust váltok. Ebben a bejegyzésben az utóbbival fogok foglalkozni, azaz azzal, hogy mikor kell térfogati, felületi és tartó elemtípus.

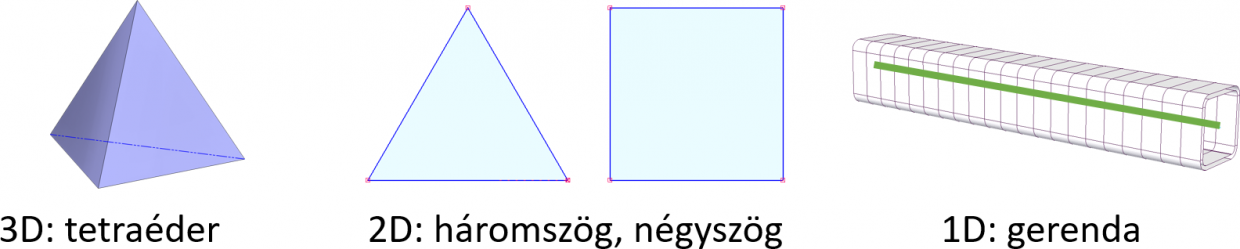
Induljunk ki egy egyszerű esetből. Van a következő képen látható lemezalkatrészem és elolvastam ennek a blogsorozatnak a második részét. A blog alapján tudom, hogy a keresztmetszetben több elemre van szükségem a feszültségkomponensek kiszámításához.

Ennek a lemez alkatrészenek a vizsgálatához, ha létrehozok egy térfogati hálót, akkor a „ritkább” háló így néz ki:

Ha ezt elkezdem sűríteni akkor eljuthatok egy olyan hálóhoz, ahol van több elem a testen belül, viszont már a hálózás is eléggé sokáig tart, így a szimuláció lefuttatása meg még tovább.

Ebben az esetben tételezzük fel, hogy a szimmetria használata nem opció, így az egész testet kell vizsgálnom, így nem marad más, mint elemtípust váltani és azzal lefuttatni a szimulációt. A különböző elemtípusok használatával a végeselemes oktatásainkon is szoktam foglalkozni, illetve az ügyféltámogatás során is elő szokott jönni, így készítettem egy Tudásbázis videót az ügyféltámogatási oldalunkra. Ezt a videót ebbe a blogbejegyzésbe is beágyaztam, így itt is megnézhető:

A videóban azt lehetett látni, hogy vannak szilárdtestek, lemezek és tartók és ezekből hogyan lehet felületmodellt készíteni és azokat hogyan lehet 2D-s elemekkel behálózni, illetve ezekkel hogyan lehet szimulációkat lefuttatni.

A videóból két dolgot emelnék ki, az egyik, hogy a vastagság virtuális és azt a szimuláció építési fájában tudjuk állítani:

A másik, hogy a lemez két oldalán az eredmények (az erőrendszertől függően) eltérhetnek, azaz külön számol a belső és a külső oldallal.

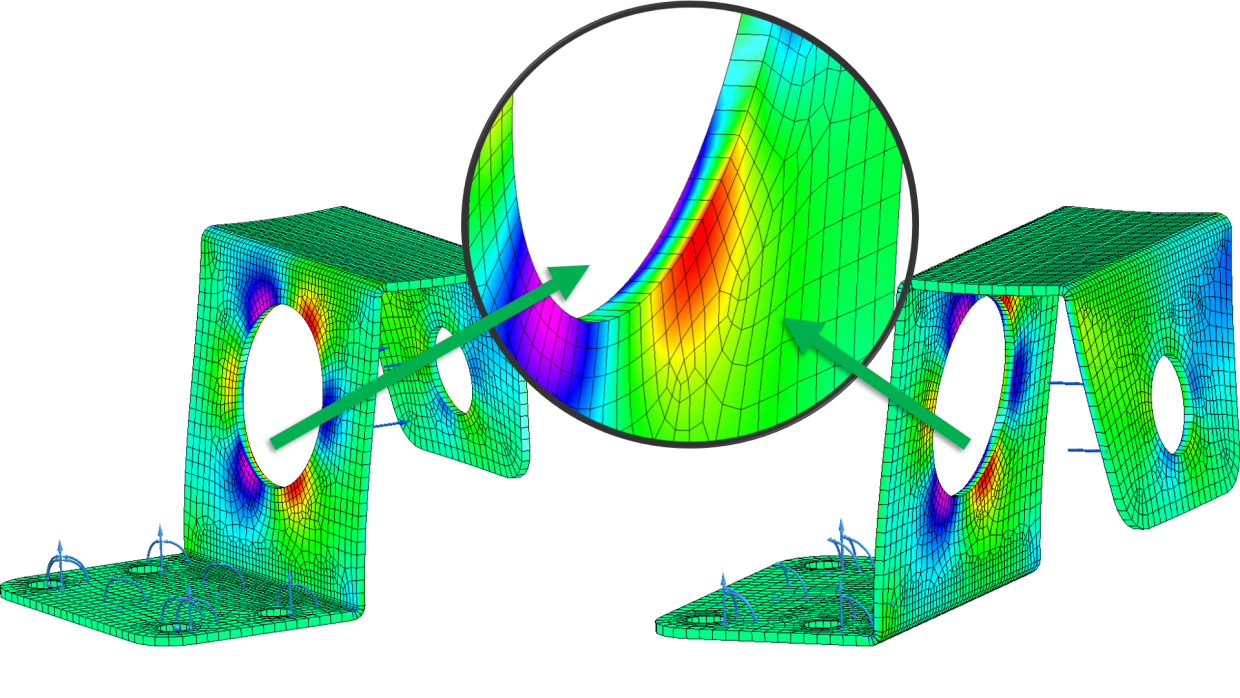
Azokban az esetekben, amikor olyan testeket vizsgálunk, mint az előző képen látható lemez, azaz a vastagsága jóval kisebb, mint a vastagságra merőleges irányok, akkor célszerű 2D-s elemeket használni. A Solid Edge Simulation-ön belül, illetve Femap-en és NX-en belül Simcenter 3D-ben is van lehetőségünk arra, hogy csak háromszög vagy négyszög elemeket használjunk, illetve megoldható az, hogy mind a kettőt.

Ennél a fajta elemtípusnál arra célszerű figyelni, hogy

• a test legyen állandó vastagságú,
• a jellemző méret legalább 10x legyen nagyobb, mint a vastagság.

Nézzük a konstans anyagvastagság a lemez alkatrészeknél megoldható, így a két következő ábrán látható test biztosan átalakítható felületmodellé és 2D-s elemekkel hálózható.

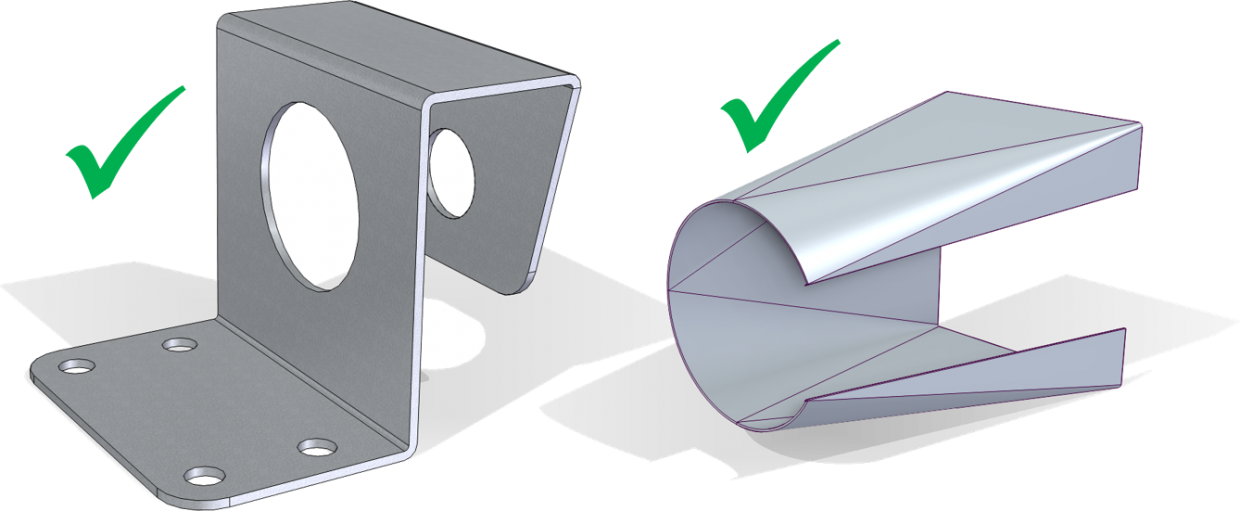
Amennyiben a következő ábrákon látható tartókat nézem, az alsó, azaz a zártszelvény átalakítható, az I és az U szelvény már kérdéses. Átalakítható felületmodellé, viszont ezeknél az elemeknél nem állandó a keresztmetszet. Ebben az esetben vagy azt csinálom, hogy a felületeket a vékonyabbra állítom be, vagy ezeket külön testként kezelem és akkor az egyik mondjuk 3 mm vastag a másik elem meg 5 mm. Utóbbi esetében a felületmodellek egymástól függetlenek, így szerelésen belül Él kapcsolattal össze kell őket „hegeszteni”.

Amennyiben a következő ábrán látható forgástestem vagy az alakos „hogyishívjákom” van, azoknál is lehet csinálni felületmodellt a testekből, csak ha azt a vastagít paranccsal visszaalakítom szilárdtesté nem a kiindulási testet kapom vissza.

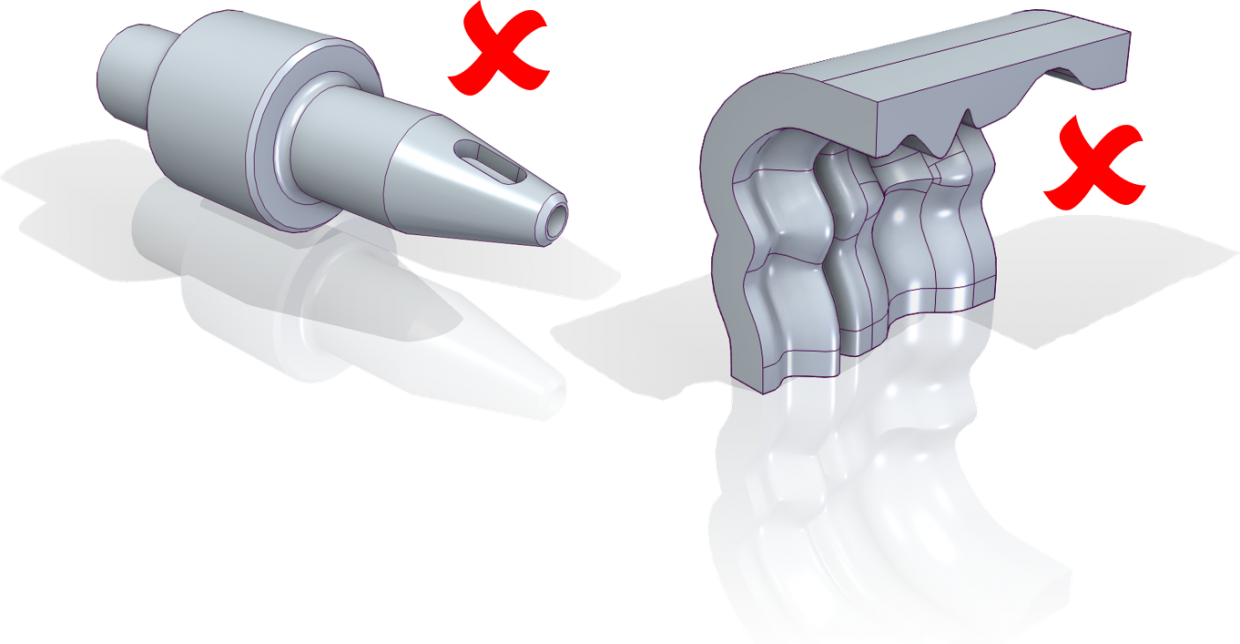
Ezekben az esetekben is elképzelhetők olyan esetek amikor 2D-s elemekkel célszerű behálózni, de általános esetekben jobb inkább térfogati elemeket használni. Viszont „Általános testek” hálótípust használva megoldható, hogy ezeket a testeket az előző lemezekkel egy szimulációban vizsgáljuk meg, azaz a 3D elemekkel hálózott testek 2D-s elemekkel hálózott testekkel együtt szimulálhatók.

Amennyiben ezek után is kell még egyszerűsíteni, akkor a szimmetria kényszert ehhez használhatjuk, viszont arra kell figyelnünk, hogy az „Elmozdulás sík mentén” csak a szilárdtestek esetén használható szimmetriaként, felületmodellek esetén a következő videóban látható felhasználói kényszert kell hozzáadnunk:

Eddig a bejegyzésben 3D-s és 2D-s elemekről volt szó, vannak még 1D-s és 0D-s elemek is. Tartószerkezetek szimulációjához ezek közül az 1D-s elemeket kell használni, mely a Tartószerkezet környezetben érhető el. Ennek módja a következő webinárban látható (1 óra, 14 perc 16 másodpercnél):

Ebben a videóban nincsen részletezve, de itt a szimuláció egy vonallal történik, aminek a tulajdonságait, azaz a keresztmetszeti jellemzőit a geometriából számolja ki a Solid Edge Simulation. Ezeket a jellemzőket a szimulációs fában (hálózás után) le is tudjuk kérdezni.

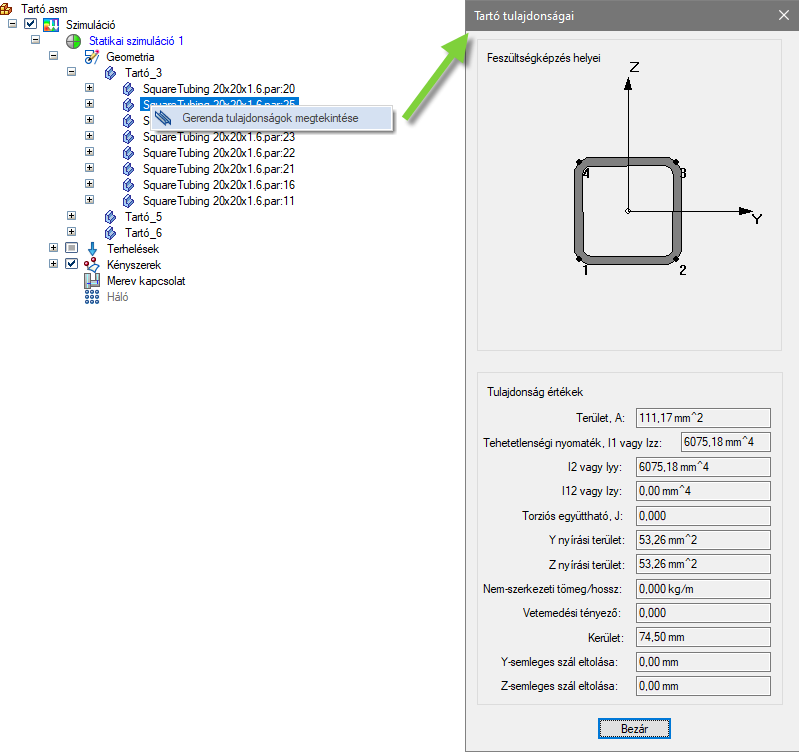
Ennél a fajta szimulációnál arra kell figyelnünk, hogy

• Akkor használjuk ezt az elemtípust, ha a tartó hossza legalább 10x nagyobb, mint a keresztmetszet mértékadó mérete.
• Hálózni itt a hossz mentén hálózunk, azaz az 1D-s elemet (vonalat) daraboljuk fel.
• Mivel az 1D-s elem csak a hosszt tartalmazza, így a sarokkezelés, furatok és bármilyen egyéb dolog, amit ráraktunk azt nincs benne a szimulációban.
• Ha megnézzük a hálót úgy tűnhet, hogy anyag az anyagban van… Ez igazából nem gond, mert itt nem az „anyaggal” számolunk, hanem az 1D-s elemmel, azaz a tartó elméleti középvonalával. Ha vonal-vonallal keresztezi egymást ott kapcsolódási csomópont lesz (ellenben anyag az anyagban lenne, khöm… vonal a vonalban).

Azt, hogy mikor mit célszerű használni, arra nagyon nehéz válaszolni. Ha van egy szerverfarmom, amin tudom futtatni a szimulációimat és az idő nem számít, akkor egyértelmű, hogy úgy kell futtatnom, ahogy nekem kényelmes, pl. mindent szilárdtestként és majd lesz rá eredményem ami, ha nem jó akkor újrafuttatom.

Amennyiben nem áll rendelkezésre végtelen idő és számolási erőforrás akkor a feladatot célszerű végig gondolni, mit szeretnék szimulálni és milyen kimenetre van szükségem.

Amennyiben tartót kell szimulálnom, én legelőször 1D-s elemekkel szoktam nekiállni a szimulációknak, itt megnézem, hogy mekkora a legnagyobb elmozdulás és a feszültség. Ez alapján, ha a tartó ránézésre megfelel, akkor a furatok és a sarokkezelés miatt felületmodellé alakítom őket és középfelülettel futtatom le a szimulációimat.

Amennyiben valamilyen lemezt kell vizsgálnom, akkor az 2D-s elem, azaz középfelület és azzal.

Ha szilárdtestjeim vannak, akkor azokat jellemzően térfogati hálóval szoktam vizsgálni, kivéve, ha a geometria, vagy az erőrendszer megengedi, hogy egyszerűsítsek felületi hálóra. Amennyiben valamilyen nagyon nemlineáris dolgot vizsgálok, abban az esetben is szeretem a szilárdtesteket felületmodellre egyszerűsíteni.

Amennyiben a szilárdtest egy tengely jellegű alkatrész és az erőendszer is olyan, hogy megtehetem, hogy síkfeszültségre, síkalakváltozásra vagy tengelyszimmetriára egyszerűsítsek, akkor átlépek Femap-be vagy Simcenter 3D-be (NX) és ott ezekkel az egyszerűsítésekkel 2D-re egyszerűsítem vissza a szimulációt és úgy futtatom le.

Az előzőek az én tippjeim és szokásiam voltak, amiket most hírtelen össze tudtam szedni. Mindegyik mögött az áll, hogy a szimulációkat minél gyorsabban szeretném lefuttatni és minél részletesebben.

A blogbejegyzésben lévő dolgok (pl. középfelületek létrehozása) mind emberidőbe telnek. Lefuttatni egy szimulációt az csak gépidő. A nagy kérdés az egyszerűsítések előtt az, hogy a gépidőt és az emberidőt mérlegelni kell, melyikkel mennyi időt nyerhetünk. Azoknak, akiknél nem végellenőrzésre használják a szimulációkat, hanem már a tervezés első szakaszától, nekik előbb látszódik az, hogy jobban megéri az emberidőt belerakni a szimuláció előkészítésébe, mint azoknál, akik végellenőrzésre használják és az eredmények természetesen „tegnapra kellenek”.

Hálózós blogsorozat részei:

• Kellően sűrű a hálóm? I.– Lokális hálósűrítés SE Simulation-ön belül
• Kellően sűrű a hálóm? II. – Most akkor legalább 3 vagy 5 elem kell?
• Kellően sűrű a hálóm? III. – Feszültség gyűjtőpontokkal és hálófüggetlenségi vizsgálat
• Kellően sűrű a hálóm? IV. – Lokális hálósűrítés és konvergencia vizsgálat FLOEFD-n belül
• Kellően sűrű a hálóm? V. – Adaptív hálósűrítés és konvergencia vizsgálat FLOEFD-n belül
• Kellően sűrű a hálóm? VI. – Időlépés meghatározása SE Motion-ben
• Kellően sűrű a hálóm? VII. – Szilárdtest, héj, tartó – elemtípusok Solid Edge Simulation-ben